確率的勾配降下法

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day56


経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0



■本日の進捗

  • 確率的勾配降下法を理解


■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

今回は、勾配降下法で交差エントロピー誤差を指標に学習できるようになったニューラルネットワークモデルを拡張して、ミニバッチ学習を適用したいと思います。

■勾配降下法による学習曲線

まずは勾配降下法を用いたニューラルネットワークの学習の様子を可視化してみたいと思います。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

def relu(x):
    return np.maximum(0, x)

def softmax(z):
    c = np.max(z, axis=1, keepdims=True)
    exp_z = np.exp(z - c)
    sum_exp_z = np.sum(exp_z, axis=1, keepdims=True)
    y = exp_z / sum_exp_z
    return y

def a(x, W, b):
    return np.dot(x, W) + b

def init_network():
    network = {}
    network['W1'] = np.random.randn(784, 50) * 0.1
    network['b1'] = np.zeros(50)
    network['W2'] = np.random.randn(50, 100) * 0.1
    network['b2'] = np.zeros(100)
    network['W3'] = np.random.randn(100, 10) * 0.1
    network['b3'] = np.zeros(10)
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = a(x, W1, b1)
    z1 = relu(a1)
    a2 = a(z1, W2, b2)
    z2 = relu(a2)
    a3 = a(z2, W3, b3)
    y = softmax(a3)

    return y

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        
        x[idx] = tmp_val + h
        fxh1 = f(x)  # f(x + h)
        
        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x - h)
        
        grad[idx] = (fxh1 - fxh2) / (2 * h)
        x[idx] = tmp_val
        it.iternext()
    
    return grad

def numerical_gradient_network(network, x, t):
    grads = {}
    
    def loss_W(W): 
        y = forward(network, x)
        return cross_entropy_error(y, t)
    
    grads['W1'] = numerical_gradient(loss_W, network['W1'])
    grads['b1'] = numerical_gradient(loss_W, network['b1'])
    grads['W2'] = numerical_gradient(loss_W, network['W2'])
    grads['b2'] = numerical_gradient(loss_W, network['b2'])
    grads['W3'] = numerical_gradient(loss_W, network['W3'])
    grads['b3'] = numerical_gradient(loss_W, network['b3'])
    
    return grads

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

print("X_train.shape :{}".format(X_train.shape))
train_size = X_train.shape[0]

batch_size = 10
np.random.seed(8)
batch_mask = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_mask]
y_batch = y_train[batch_mask]

lr = 0.01
step_num = 1000 
network = init_network()
loss_history = []

for i in range(step_num):
    grads = numerical_gradient_network(network, X_batch, y_batch)
    
    for key in ('W1', 'b1', 'W2', 'b2', 'W3', 'b3'):
        network[key] -= lr * grads[key]

    y = forward(network, X_batch)
    loss = cross_entropy_error(y, y_batch)
    loss_history.append(loss)
    print(f"Step {i+1}, Loss: {loss}")

plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("Loss 1000 steps learning")
plt.show()

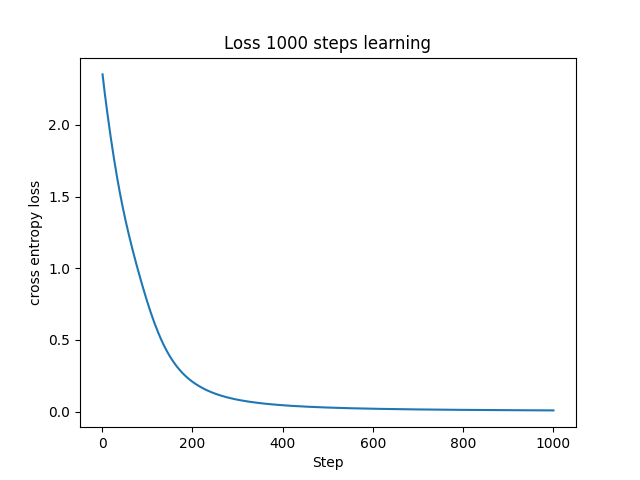
コマンドラインの出力は冗長なので省略させていただきます。損失関数の値は綺麗な曲線を描いて非常に小さい値に収束しています。ニューラルネットワークが良くデータを学習できていることが分かりました。

■確率的勾配降下法

確率的勾配降下法（stochastic gradient descent：SGD）とは、確率的に選ばれたデータに対して行う勾配降下法で、各ステップごとにミニバッチを選びなおして勾配を更新します。

先程の勾配降下法をSGDにするのはとても簡単で、ミニバッチの選択を勾配降下法のループ内に入れてしまえばいいだけです。これで全ステップにおいて異なるミニバッチが確率的にランダムに選ばれるミニバッチ学習を用いた確率的勾配降下法を実装することができます。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

def relu(x):
    return np.maximum(0, x)

def softmax(z):
    c = np.max(z, axis=1, keepdims=True)
    exp_z = np.exp(z - c)
    sum_exp_z = np.sum(exp_z, axis=1, keepdims=True)
    y = exp_z / sum_exp_z
    return y

def a(x, W, b):
    return np.dot(x, W) + b

def init_network():
    network = {}
    network['W1'] = np.random.randn(784, 50) * 0.1
    network['b1'] = np.zeros(50)
    network['W2'] = np.random.randn(50, 100) * 0.1
    network['b2'] = np.zeros(100)
    network['W3'] = np.random.randn(100, 10) * 0.1
    network['b3'] = np.zeros(10)
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = a(x, W1, b1)
    z1 = relu(a1)
    a2 = a(z1, W2, b2)
    z2 = relu(a2)
    a3 = a(z2, W3, b3)
    y = softmax(a3)

    return y

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        
        x[idx] = tmp_val + h
        fxh1 = f(x)  # f(x + h)
        
        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x - h)
        
        grad[idx] = (fxh1 - fxh2) / (2 * h)
        x[idx] = tmp_val
        it.iternext()
    
    return grad

def numerical_gradient_network(network, x, t):
    grads = {}
    
    def loss_W(W): 
        y = forward(network, x)
        return cross_entropy_error(y, t)
    
    grads['W1'] = numerical_gradient(loss_W, network['W1'])
    grads['b1'] = numerical_gradient(loss_W, network['b1'])
    grads['W2'] = numerical_gradient(loss_W, network['W2'])
    grads['b2'] = numerical_gradient(loss_W, network['b2'])
    grads['W3'] = numerical_gradient(loss_W, network['W3'])
    grads['b3'] = numerical_gradient(loss_W, network['b3'])
    
    return grads

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

print("X_train.shape :{}".format(X_train.shape))
train_size = X_train.shape[0]

batch_size = 10
np.random.seed(8)

lr = 0.01
step_num = 1000 
network = init_network()
loss_history = []

for i in range(step_num):

    batch_mask = np.random.choice(train_size, batch_size)
    X_batch = X_train[batch_mask]
    y_batch = y_train[batch_mask]

    grads = numerical_gradient_network(network, X_batch, y_batch)
    
    for key in ('W1', 'b1', 'W2', 'b2', 'W3', 'b3'):
        network[key] -= lr * grads[key]

    y = forward(network, X_batch)
    loss = cross_entropy_error(y, y_batch)
    loss_history.append(loss)
    print(f"Step {i+1}, Loss: {loss}")

plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("Loss SGD")
plt.show()

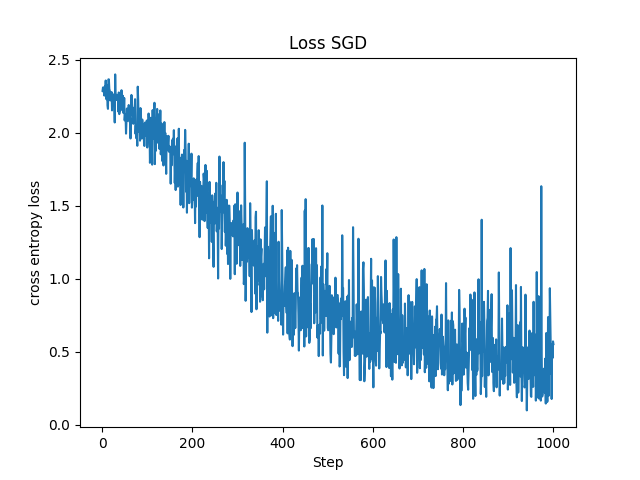
先程の勾配降下法に比べて損失関数の値が揺れていて収束性はあまり良くないです。やはり決まったミニバッチで学習する場合に比べて収束性は劣り、最悪の場合は発散する恐れもありますが、それでも60000個のデータから10個のみを抽出した勾配降下法に比べて計算コストはほとんど変わらずに（今回の場合には確率的に最大で）10000個のデータを用いて学習する確率的勾配降下法の方がデータの特徴を良く捉えられる可能性が高いと言えます。

■おわりに

これまで学んできた手法をすべて用いて、計算コストをほとんど変えることなく圧倒的に多くのデータを用いてパラメータを学習することができるニューラルネットワークのモデルを構築することができました。

ミニバッチ学習の実装は、通常のミニバッチ化と比べてソースの記述自体はほとんど変わらないのでここまで簡単に多くのデータを使えるなら活用しない手はないと思います。一方で収束性はかなり悪くなるので、もう少しイタレーション回数を増やしてみたり、内部的なイタレーションを導入してみて様子を見てみるのも面白そうです。

■参考文献

  1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
  2. 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
  3. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
  4. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html

hammertime

, ,
, , , ,

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です