AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day32
経緯についてはこちらをご参照ください。
■本日の進捗
●グリッドサーチを理解
●ランダムサーチを理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
これまでも何度か調整を行ってきたハイパーパラメータに関する単純な場合の最適化手法を学んでいきます。
■グリッドサーチ
グリッドサーチ(grid search)とは、機械学習モデルのハイパーパラメータの最適化に用いられる手法で、パラメータの全通りの組み合わせに対してモデルを学習させて最適なパラメータセットを見つける方法です。
単純なグリッドサーチでは、テストデータに対して最高の性能を出したパラメータの組み合わせを最適解として知ることができます。
この場合のグリッドサーチはみんな大好きfor文を使って記述することができます。
ワインデータセットに対してガウシアンカーネル法サポートベクターマシンを最適化していきたいと思います。(ここでSVCを選んだ理由は単にハイパーパラメータが多くて面白いからです。)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
data = load_wine()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=8)
param_grid = {
'C': [0.1, 1, 10, 100],
'gamma': [1, 0.1, 0.01, 0.001]
}
scores = []
for C in param_grid['C']:
row = []
for gamma in param_grid['gamma']:
model = SVC(C=C, gamma=gamma, kernel='rbf')
model.fit(X_train, y_train)
score = model.score(X_test, y_test)
row.append(score)
scores.append(row)
scores = np.array(scores)
plt.figure(figsize=(8, 6))
plt.imshow(scores, interpolation='nearest', cmap='viridis', vmin=0.4, vmax=0.8)
plt.title('Grid Search (C - Gamma)')
plt.xlabel('Gamma')
plt.ylabel('C')
plt.xticks(np.arange(len(param_grid['gamma'])), param_grid['gamma'])
plt.yticks(np.arange(len(param_grid['C'])), param_grid['C'])
plt.colorbar(label='Accuracy')
plt.show()
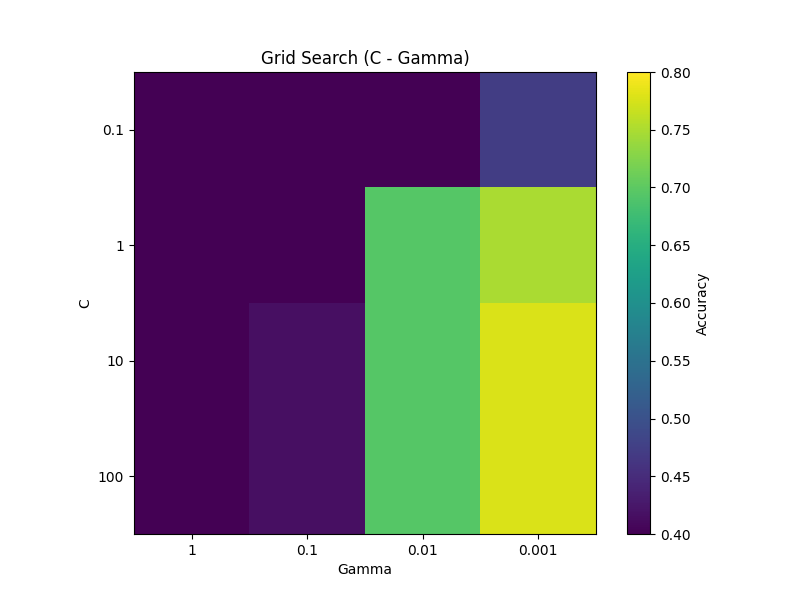
このように可視化することでどのCとGammaの組み合わせが良いかがよくわかります。
傾向的にCは値が大きい方が、Gammaは値が小さい方がAccuracyが良くなることが分かります。ここで選ぶならC=100, Gamma=0.001辺りでしょうか。
■ランダムサーチ
単純なグリッドサーチの問題点は、(後述の通りクリティカルな問題点もあるがここでは置いておいて)無駄な計算が多いことです。改めてグリッドサーチによるヒートマップを見てみると、左上の方はほとんど機能していません。この辺りはこんなに丁寧に見る必要がないかもしれません。
これを解消するのがランダムサーチ(random search)と呼ばれる手法です。やることは単純で、上記のグリッドサーチで定義したパラメータセットに対して、任意の試行回数分ランダムに試してみるだけです。
ランダムサーチの注意点は乱数性がありどのパラメータの組み合わせを試すのかは一定ではないことだと言われています。しかしここでの目的を「最適解を探索する」ではなく「最適化に向けたあたりをつける」と考えれば全く問題はありません。
先ほどのグリッドサーチは16通りの組み合わせを試しましたが、その半分である8通りの試行回数であたりを付けてみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
import random
data = load_wine()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=8)
param_grid = {
'C': [0.1, 1, 10, 100],
'gamma': [1, 0.1, 0.01, 0.001]
}
n_iterations = 8
random_combinations = []
scores = []
for _ in range(n_iterations):
C = random.choice(param_grid['C'])
gamma = random.choice(param_grid['gamma'])
random_combinations.append((C, gamma))
model = SVC(C=C, gamma=gamma, kernel='rbf')
model.fit(X_train, y_train)
score = model.score(X_test, y_test)
scores.append(score)
scores = np.array(scores)
C_values, gamma_values = zip(*random_combinations)
plt.figure(figsize=(8, 6))
sc = plt.scatter(gamma_values, C_values, c=scores, cmap='viridis', s=100, edgecolors='k', vmin=0.4, vmax=0.8)
plt.title('Random Search (Gamma - C)')
plt.xlabel('Gamma')
plt.ylabel('C')
plt.xscale('log')
plt.yscale('log')
plt.xticks(param_grid['gamma'])
plt.yticks(param_grid['C'])
plt.gca().invert_xaxis()
plt.gca().invert_yaxis()
plt.colorbar(sc, label='Accuracy')
plt.show()
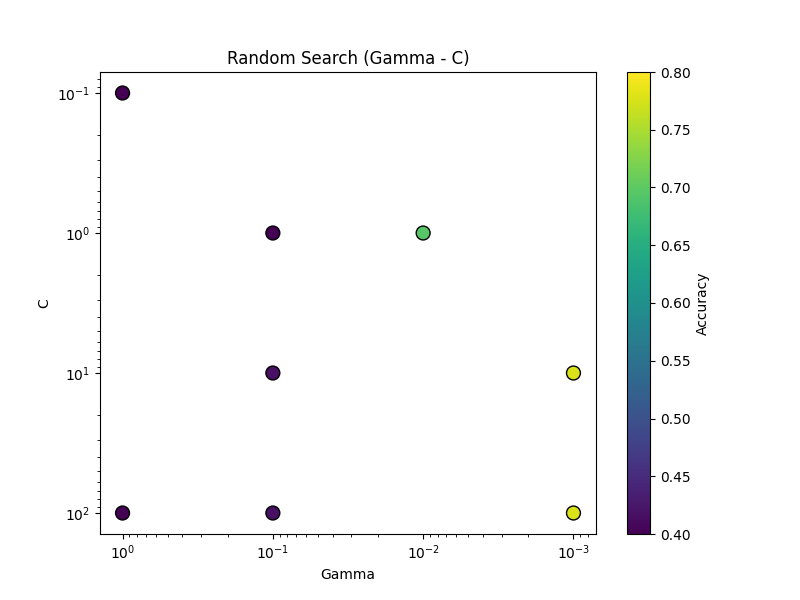
半分しかモデルを作っていませんが、どこを攻めればいいのかは一目瞭然です。先ほどと同様にCを大きく、Gammaを小さくすると良さそうなので、右下あたりでグリッドサーチをかければ最適解を得られそうです。
え?コードを書き替えてる暇があったら最初からグリッドサーチで手当たり次第に見た方が早いって?
趣きがないなぁ…
■単一テストデータと最適解の危険性
これまで見てきたグリッドサーチやランダムサーチによる最適化のおかげで、データセットに対するハイパーパラメータの最適解が分かりました(と言わせてください、今だけは)。
これらの手法はとても簡単で可視化もできますが、この使い方には前回学んだ学習モデルの評価と同じ危険性が潜んでいます。
単一のテストデータで最適化する場合、そのテストデータの取り方(一般的には乱数性がある)によってはその偏りの影響を強く受け、テストデータに過剰適合し汎化性能が損なわれる危険があります。つまりテストデータバイアスがかかるリスクを伴うわけです。
簡単に言うと、そのただ一つのテストデータで性能が出たからといって、他のデータに対して必ずしも最適なハイパーパラメータではないよね?ということです。
この問題を解消するにはモデルの評価にも用いた交差検証とグリッドサーチを組み合わせる方法が良く知られていますが、この内容は次回学んでいきたいと思います。
■おわりに
機械学習モデルの目指すところは、初めて見るデータに対してできるだけ正確に予測できることにあります。つまり現在手持ちのデータが訓練データなのかテストデータなのかに依らず、結局のところそのデータに関する(直接的な)性能には興味がないのです。
大事なのは汎化性能です。限られたデータの中でどうすれば汎化性があると言えるのかどうか、先駆者達の考えが垣間見えるモデル評価手法とパラメータ最適化手法。単純ですがかなり面白いです。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html