AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day24
経緯についてはこちらをご参照ください。
■本日の進捗
●ビニングを理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
今回も特徴量エンジニアリングを学んで、機械学習アルゴリズムとは別の角度からモデル精度向上を目指していきたいと思います。
■ビニング
ビニング(Binning)とは連続値特徴量を離散的にカテゴリに分解する手法です。一見複雑に見える数値データを単純化して精度を上げたりデータを理解しやすい形に変換します。単純にすることで過剰適合を抑制することもできます。
ビニングはターゲット変数に対して非線形な連続値特徴量に効果的なので、まずはsin波を作って線形回帰でその純粋な実力を見てみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
plt.scatter(X, y, color='orange')
plt.plot(X, y_pred, color='green')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.show()
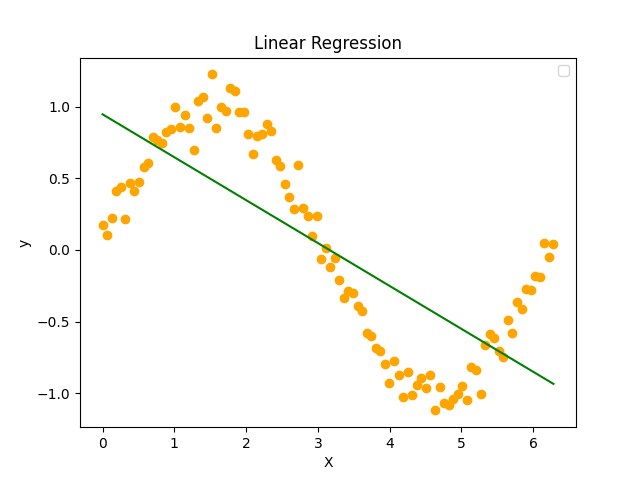
このようなデータに対しては線形回帰の得意とするものではないため、データの特徴をほとんど捉えることができていません。
特徴量xの0から6までを10個のビンに分割して線形回帰モデルを学習しなおしてみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import OneHotEncoder
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
bins = np.linspace(0, 6, 11)
which_bin = np.digitize(X, bins=bins)
encoder = OneHotEncoder(sparse_output=False)
X_binned = encoder.fit_transform(which_bin)
model_binned = LinearRegression()
model_binned.fit(X_binned, y)
y_binned_pred = model_binned.predict(X_binned)
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
plt.scatter(X, y, color='orange')
plt.plot(X, y_pred, color='green')
plt.plot(X, y_binned_pred, color='red', label='binned')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Binned Data')
plt.show()
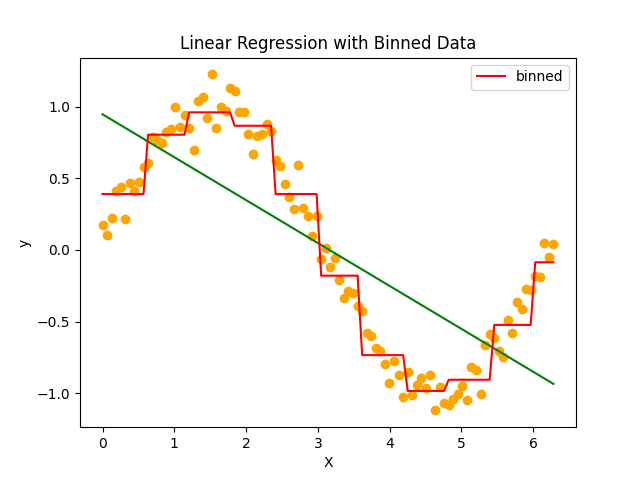
10個に区切ったそれぞれのビンを特徴量として、ワンホットエンコーディングを適用してビンに対して線形回帰を実施しています。これだけの前処理で見事に線形モデルで学習させることに成功しています。
ビンの数を変えることで容易にモデル粒度を変更することもできそうです。
決定木に対する挙動も見てみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
model = DecisionTreeRegressor(max_depth=8)
model.fit(X, y)
y_pred = model.predict(X)
plt.scatter(X, y, color='orange', alpha=0.5)
plt.plot(X, y_pred, color='green')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Decision Tree Regression')
plt.show()
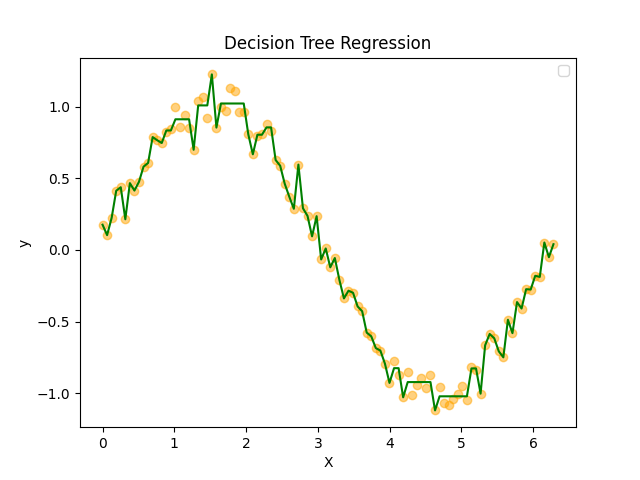
適当な設定ですが、さすがは決定木アルゴリズム、予測精度も過剰適合具合も凄まじいです。
線形回帰と同様にビニングを行ってみると学習モデルはどう変わるのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import OneHotEncoder
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
model = DecisionTreeRegressor(max_depth=8)
model.fit(X, y)
y_pred = model.predict(X)
bins = np.linspace(0, 6, 11)
which_bin = np.digitize(X, bins=bins)
encoder = OneHotEncoder(sparse_output=False)
X_binned = encoder.fit_transform(which_bin)
model_binned = DecisionTreeRegressor(max_depth=8)
model_binned.fit(X_binned, y)
y_pred_binned = model_binned.predict(X_binned)
plt.scatter(X, y, color='orange', alpha=0.5)
plt.plot(X, y_pred, color='green')
plt.plot(X, y_pred_binned, color='red', label='binned')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Decision Tree Regression')
plt.show()
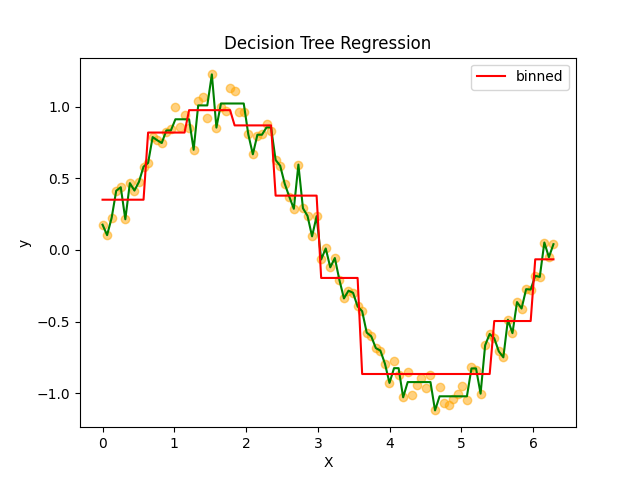
過剰適合は改善しましたが、これは決定木のパラメータでも対応できそうです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import OneHotEncoder
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
model = DecisionTreeRegressor(max_depth=3)
model.fit(X, y)
y_pred = model.predict(X)
bins = np.linspace(0, 6, 11)
which_bin = np.digitize(X, bins=bins)
encoder = OneHotEncoder(sparse_output=False)
X_binned = encoder.fit_transform(which_bin)
model_binned = DecisionTreeRegressor(max_depth=8)
model_binned.fit(X_binned, y)
y_pred_binned = model_binned.predict(X_binned)
plt.scatter(X, y, color='orange', alpha=0.5)
plt.plot(X, y_pred, color='green')
plt.plot(X, y_pred_binned, color='red', label='binned')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Decision Tree Regression')
plt.show()
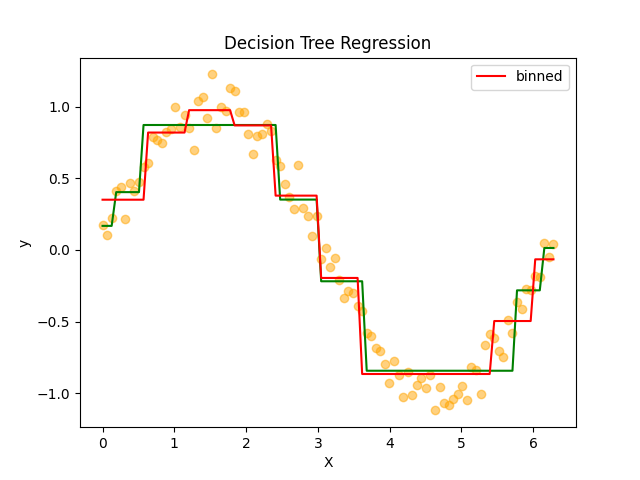
事前枝刈りを実施してmax_depthを3まで減らすことで、モデルの複雑度を大幅に下げて、ビニングをした場合と近い粒度でのモデルを作ることができました。
■おわりに
線形モデルに対してはビニングは絶大な効果があることが分かりました。通常は線形回帰で予測が難しいような複雑なデータセットに対しても簡単に適用でき、その粒度すらも簡単に調節できそうです。特徴量エンジニアリングが時に機械学習アルゴリズムよりも重要と言われる理由が良く示されていると思います。
また、決定木に関してもある程度の効果はありましたが、事前枝刈りで十分対応可能な範囲での限定的な効果しかありませんでした。これはビニングに効果がないというよりもむしろ、決定木がビニングを行うのと同程度の学習を自動で行っていると言えそうです。
決定木、改めて恐るべしですね。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html