AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day20
経緯についてはこちらをご参照ください。
■本日の進捗
●k-meansクラスタリングを理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
今回は教師なし学習の中でもデータセットの中で似ているデータポイントをクラスタと呼ばれるグループに分類するための隠れたパターンや構造を見つける手法であるクラスタリング(Clustering)を学んでいきます。クラスタリングの中でも最も単純かつ広く用いられているk-meansクラスタリングを取り上げます。
■k-meansクラスタリング
基本的な考え方はk-NNにとても似ていて、データポイントの中で近い領域を代表するクラスタセンター(クラスタ重心、クラスタ中心、またはセントロイド)を設定し、k個のクラスタを作ります。
最初のクラスタセンターは乱数で選択され、k個の初期クラスタセンターを作成します。ユークリッド距離などの測定方法で距離を測定し、各データを最も近いクラスタセンターに割り当てます。これを何度も繰り返し、クラスタセンターが変化しなくなったら終了します。
計算が速く大規模データセットにも良く適用できますが、事前に適切なk値を設定する必要がある他、初期クラスタセンターの設定により結果に乱数性があります。また、クラスタサイズが一定していない不均一なデータセットは苦手にしています。
まずはあやめデータセットに対してk=3でk-meansクラスタリングを実施して挙動を見てみます。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
iris = load_iris()
X = iris.data
y = iris.target
kmeans = KMeans(n_clusters=3, random_state=8)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
plt.figure(figsize=(8, 6))
for i in range(3):
plt.scatter(X[labels == i, 0], X[labels == i, 1], label=f'Cluster {i+1}')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, label='Centroids')
plt.title(f'K-means Clustering')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.legend()
plt.show()
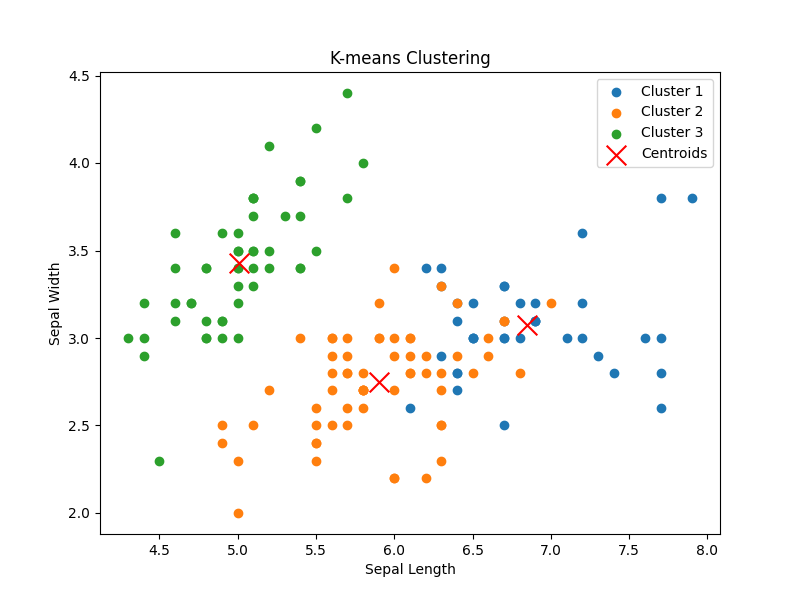
k個(ここでは3個)のクラスタセンター(Centroids)が各クラスタの重心に置かれていることが分かります。ただ、元のデータポイントの分布に互いに入り混じっている個所がありそうです。
元データと比較してみましょう。
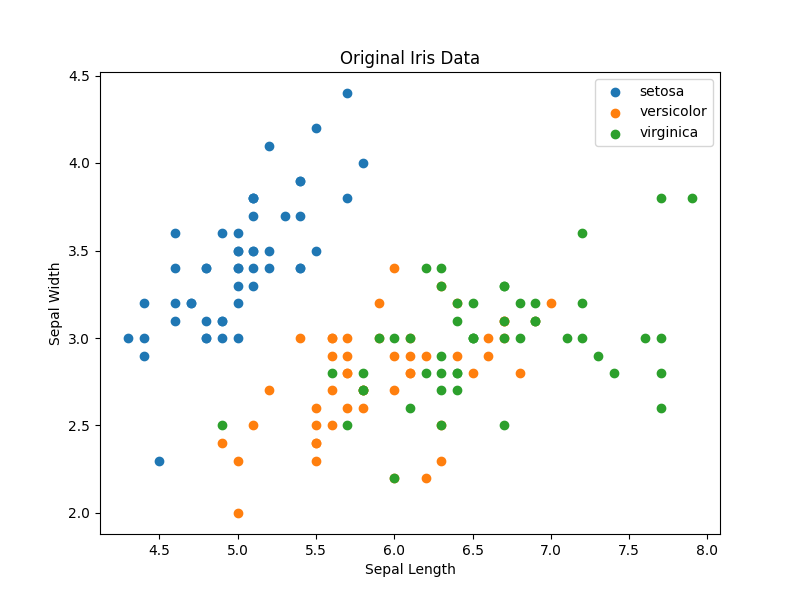
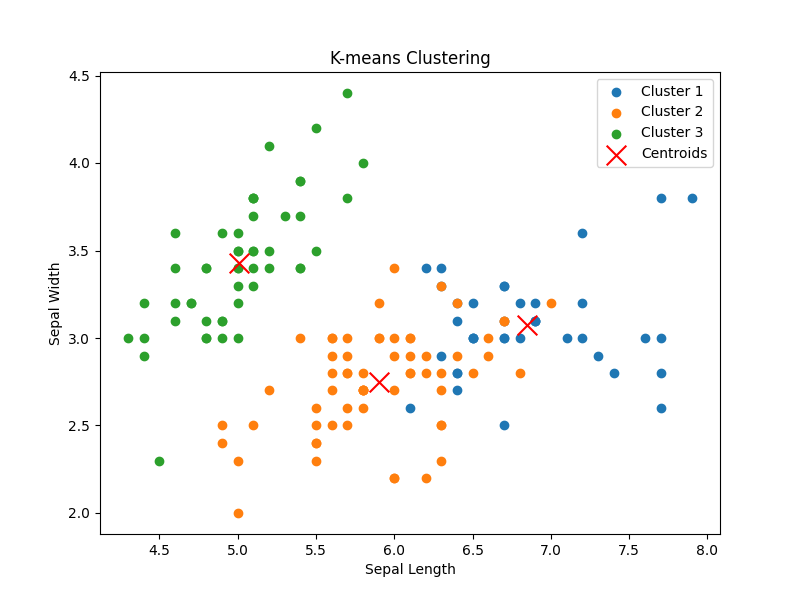
versicolorとvirginicaのデータポイントが入り混じっている個所が確認できます。この特徴量ではk-meansクラスタリングはかなりクラスタリングをするのが難しそうで、明らかな誤分類(誤クラスタ?)が発生しています。また重要なことは、これが教師なし学習であるので、クラスタのラベルは分類とは違い意味を持たないということです。Cluster1が青(のクラスタ)で、Cluster2がオレンジ、Cluster3が緑であることはただの偶然で、乱数によりラベルは都度変化します。
全特徴量に対してもクラスタリング結果を見てみましょう。
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from itertools import combinations
iris = load_iris()
X = iris.data
kmeans = KMeans(n_clusters=3, random_state=8)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
features = ['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width']
feature_combinations = list(combinations(range(4), 2))
fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(15, 12))
axes = axes.ravel()
for i, (f1, f2) in enumerate(feature_combinations):
ax = axes[i]
for cluster in range(3):
ax.scatter(X[labels == cluster, f1], X[labels == cluster, f2], label=f'Cluster {cluster+1}')
ax.scatter(centers[:, f1], centers[:, f2], c='red', marker='x', s=200, label='Centroids')
ax.set_xlabel(features[f1])
ax.set_ylabel(features[f2])
ax.set_title(f'{features[f1]} vs {features[f2]}')
plt.suptitle('K-means Clustering', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()

あやめデータセットは難しそうです。setosa(今回のクラスタでは緑色)は上手くクラスタを作れていますが、切り分けの難しい他の2つはかなり怪しいです。
また、今回はクラスが全部で3つと分かっていましたが、もしわからない場合には、k=2などを設定してしまうかもしれません。
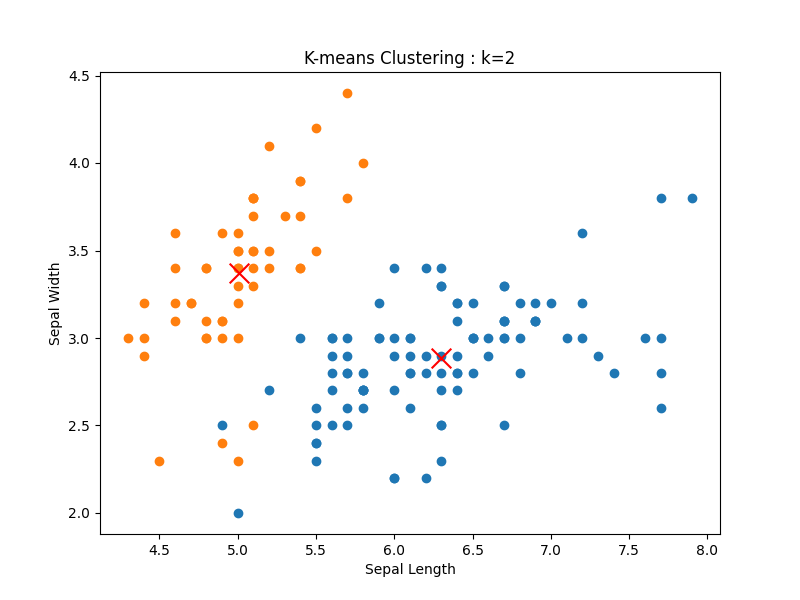
■ベクトル量子化
サンプルをもう一つ。以前も用いたmake_circlesデータセットで作った複雑な非線形データに対してもk-meansクラスタリングを実施してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
kmeans = KMeans(n_clusters=2, random_state=8)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=labels, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, label='Centroids')
plt.legend(handles=scatter.legend_elements()[0], labels=['Cluster 0', 'Cluster 1'], title='Clusters')
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.show()
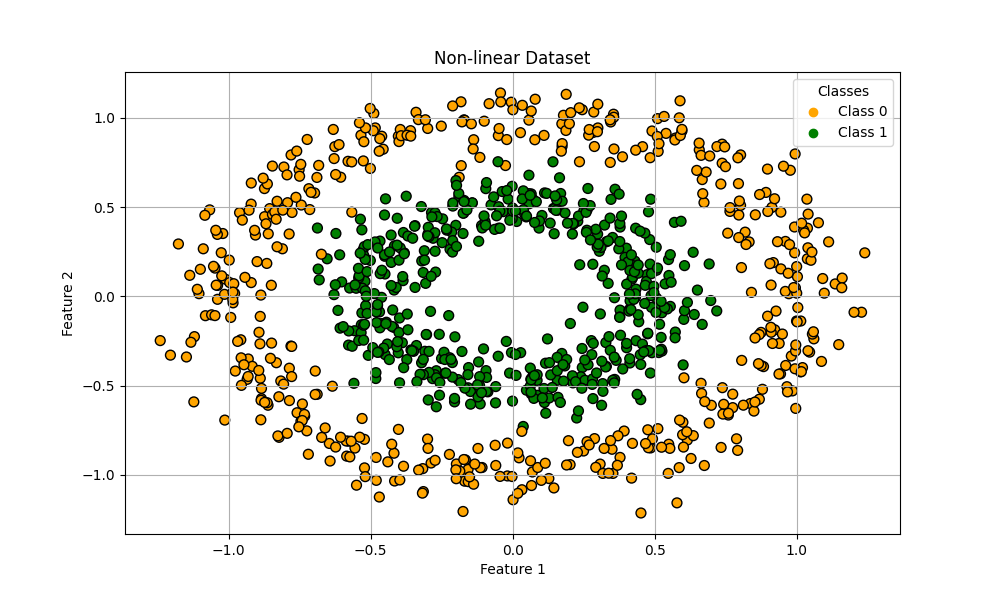
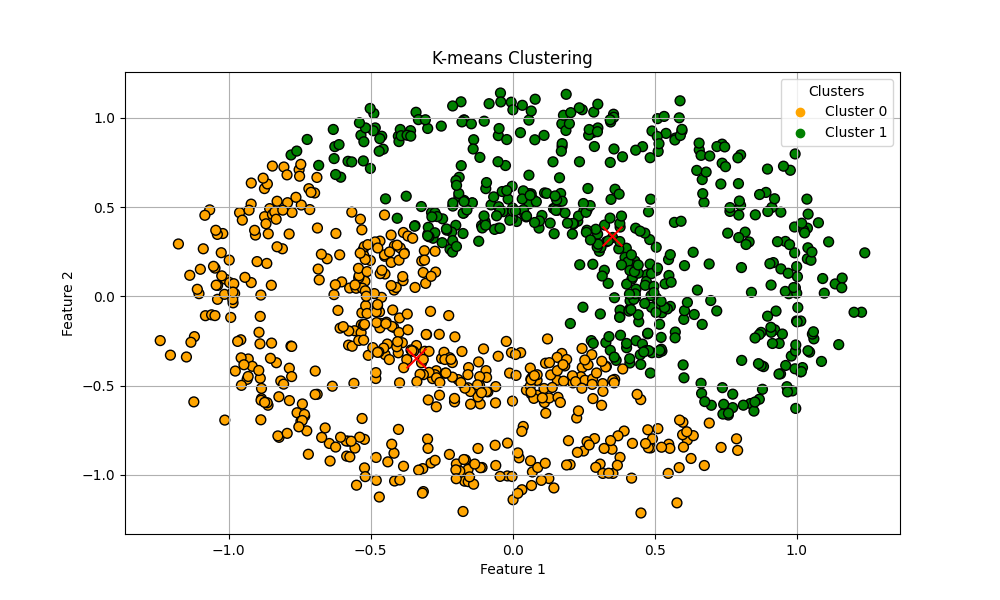
予想通りの結果です。k-meansクラスタリングはデータポイント同士の距離を測って仲間を探していくので、このように分離してはいるが距離が近い複雑なデータセットに対して上手くクラスタを作ることは難しいです。
k-meansクラスタリングはクラスタセンターを単一成分として個々のデータポイントを分解する成分分解手法と考えることができ、これをベクトル量子化(Vector Quantization:VQ)と言います。k-meansクラスタリングはデータセットの特徴量の数より多いクラスタでデータを表現できることが大きな強みです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
kmeans = KMeans(n_clusters=16, random_state=8)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=labels, cmap=plt.cm.get_cmap('hsv', 16), edgecolors='k', s=50)
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, label='Centroids')
plt.legend(handles=scatter.legend_elements()[0], labels=[f'Cluster {i}' for i in range(16)], title='Clusters', loc='upper left', bbox_to_anchor=(1.05, 1))
plt.title('K-means Clustering (k=16)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.tight_layout()
plt.show()
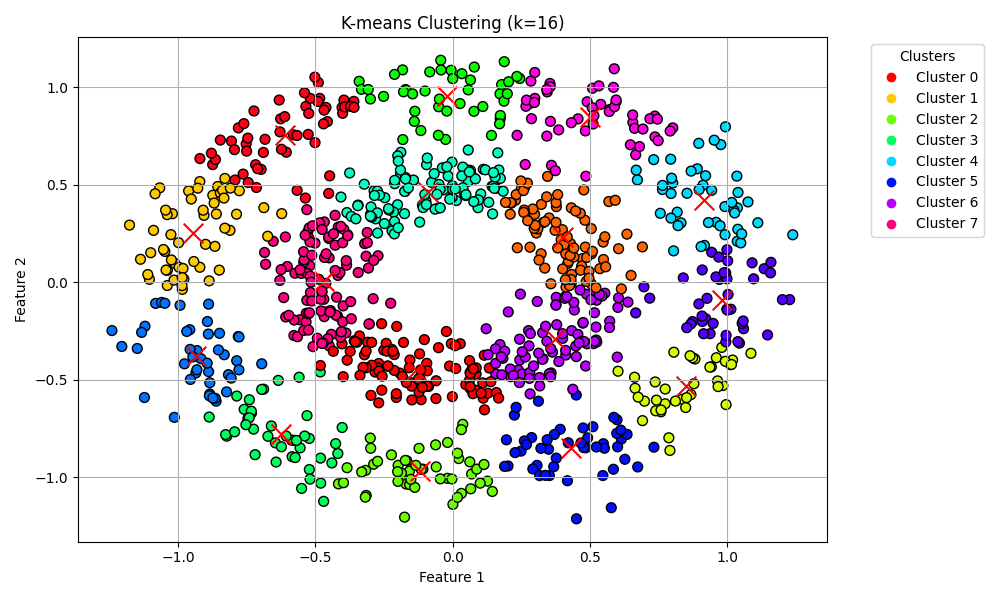
16のクラスタに分解するとかなり良くクラスタを作れています。僕たちはこのデータセットのラベルが2つであることを知っているので、すぐさま2つに分類することができます。
■おわりに
今回は教師なし学習としてk-meansクラスタリングを触ってみました。
このアルゴリズムは挙動が非常に理解しやすく、実装も簡単で学習も早いのですが、クラスタを作成する前提としてその数(k)と形状に対して強い制約があります。
この制約に当てはまらないデータセットに対してはあまり上手にクラスタを作成できないことを経験しましたが、クラスタの数(k)を特徴量の数に寄らず増やしていくことで、上手くデータを分解できることも経験しました。
上手く使いこなせればデータを理解したり整理すること、そして訓練データを作ることに大きなメリットがありそうです。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html