t分布型確率的近傍埋め込み法

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day19

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

●t-SNEを理解

■はじめに

引き続き「Pythonではじめる機械学習（オライリー・ジャパン）」で学んでいきます。

今回は前処理としても優秀なPCAやNMFとは異なり、高次元データの可視化を目的としたt-SNEを学んでいきます。

■t-SNE

t-SNE（t-distributed Stochastic Neighbor Embedding）とは、高次元データから2次元程度に次元削減を行い、データの理解のための可視化を目的とする多様体学習アルゴリズム（manifold learning algorithms）の一種です。

訓練データを変換することはできますが、教師あり学習のように学習したモデルを用いて新たな予測を行うことはできません。そのため前処理として用いることもほぼありません。

特徴的なのは、複雑な元データの構造を保ち、近いデータを低次元でも近くに配置するように次元を落とす挙動を取ることです。視覚的にも理解しやすく可視化に適しています。

高次元空間においてはデータポイント間の距離を用いて条件付き確率を計算しています。データポイントが近傍にあるほど確率が高くなり、ガウス分布が用いられます。

$$ p_{j|i} = \frac{\exp (\frac{-||x_i – x_j||^2 }{2\sigma_i^2})}{ \displaystyle \sum_{k\neq i} \exp(\frac{-||x_i – x_k||^2}{2\sigma_i^2}) } $$

この確率を算出するのに近傍のデータポイントの数を制御して、局所的にどの程度細かく見るかを調節するのにperplexityというパラメータがあります。

まずは64次元のdigitsデータセットに対してt-SNEを適用して、2次元空間に縮小して可視化してみましょう。

一般的に、t-SNE > NMF > PCA　の順番で重い（特にt-SNEは非線形）と言われているので並列化していますが、このデータセットに対してはそんなに重くないです。

from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

digits = load_digits()
X = digits.data
y = digits.target

tsne = TSNE(n_components=2, perplexity=30, random_state=8, n_jobs=-1)

X_tsne = tsne.fit_transform(X)

plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10', marker='o')
plt.colorbar(scatter)
plt.title('t-SNE Digits')
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.show()

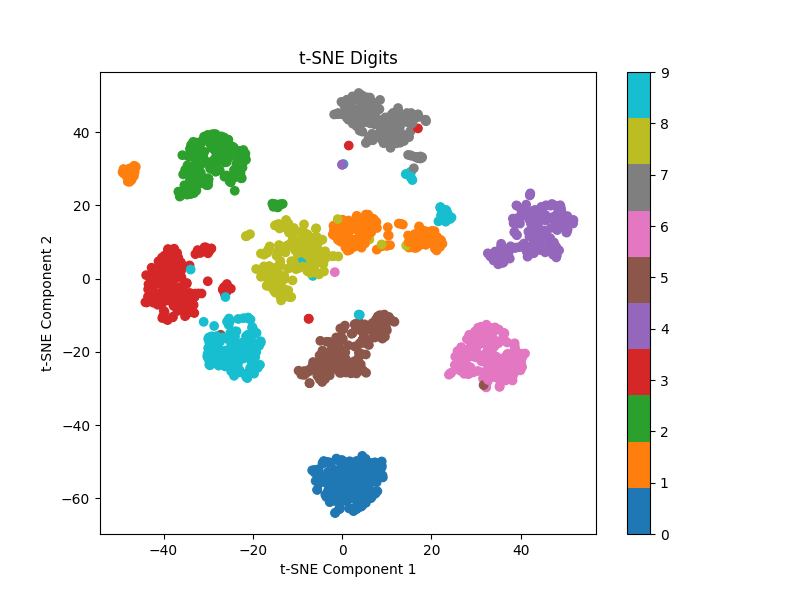
とっても簡単なのにとてつもない精度です。教師なし学習なのでもちろん各データポイントがどの数字なのかは教えていません。それでも多少の誤分類（分類ではないのだが）はあるもののほぼ完璧にデータを分離しています。手書きの数字の8×8ピクセルの画像でこの精度は驚異的と言っていいと思います。もう一度言いますが、こちらからは何も教えてないんですよ？

逆に低次元データセットに対してはあまり有効ではない（効果がないわけではない）と言われています。4特徴量しかないあやめデータセットに対して、2次元に落とす場合をPCAとt-SNEで比較して確認してみます。

from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

iris = load_iris()
X = iris.data
y = iris.target

tsne = TSNE(n_components=2, random_state=8)
X_tsne = tsne.fit_transform(X)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
ax1.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='viridis')
ax1.set_title('t-SNE Iris')

ax2.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
ax2.set_title('PCA Iris')

plt.show()

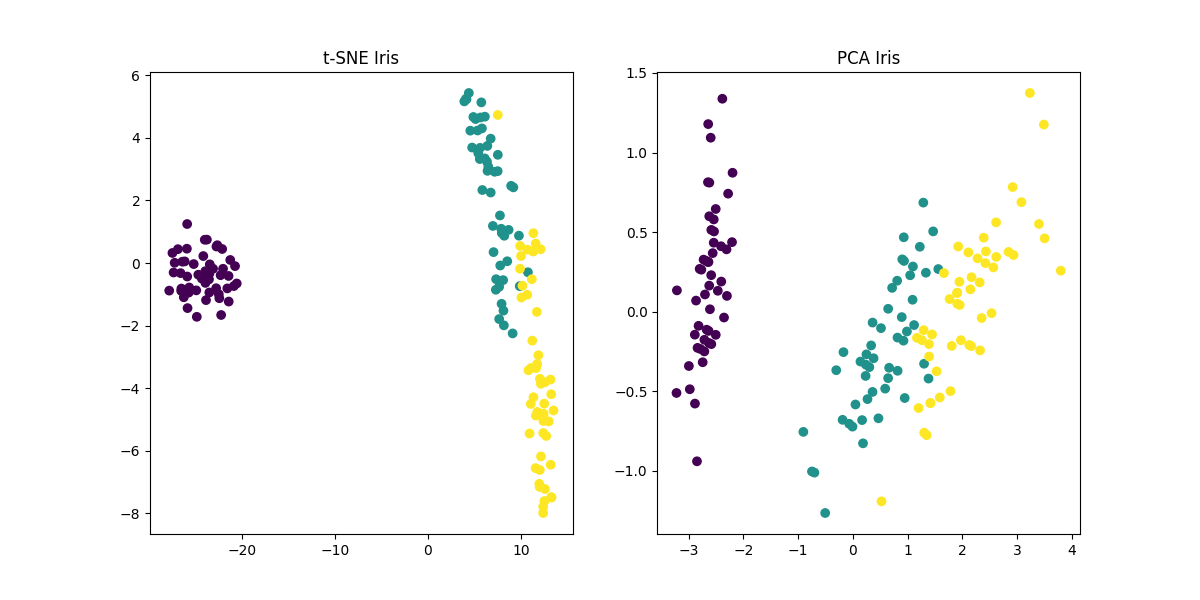
あまり効果的でないどころかPCAの方が上手く分離できていそうです。

■おわりに

かなり短いですが、低次元データセットと（比較的）高次元データセットにt-SNEを適用してみて、その性能を見てみました。低次元ではデータがそれほど複雑ではなく局所類似性を保ちつつ低次元に埋め込むt-SNEとの相性はそれほど良くなかったです。

しかし高次元データセットに適用した際の効果は目を見張るものがあり、これまで見てきたアルゴリズムの中でもかなりの精度で特徴を捉えていました。

PCAやNMFでは特徴を捉えきれないような複雑で高次元なデータセットを人間が目視で理解できるデータに落とし込む場合に真価を発揮することでしょう。

そして何より答えを教えていない状態でここまで特徴を捉えてデータを分離する性能には感動すら覚えました。ライブラリを単純に適用しただけでこの性能、先の学習が益々楽しみです。

■参考文献

Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田秀基訳. オライリー・ジャパン. 2017. 392p.
ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html