世界は点と線で出来ている

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day11


経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

●線形モデルを使ってみる

■はじめに

今回は100年前には既に誕生していたと言われる線形モデルについて勉強していきます。

■線形回帰

まずはscikit-learn標準データセットであるCalifornia housingデータセットを使って線形回帰（通常最小二乗法：OLS）を適用していきます。

線形モデルによる回帰問題で一般的な予測式は下記の通り

$$ \hat{y} = w[0] \times x[0] + w[1] \times x[1] + \cdots + w[[p] \times x[p] + b $$

xはあるデータポイントの特徴量で、w（傾き）とb（切片）は学習されたモデルのパラメータとなります。

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

data = fetch_california_housing()
X = data.data
y = data.target

X_medinc = X[:, [0]]

X_train, X_test, y_train, y_test = train_test_split(X_medinc, y, test_size=0.3, random_state=8)

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

linear_model = LinearRegression()
linear_model.fit(X_train_scaled, y_train)

y_pred = linear_model.predict(X_test_scaled)

print("train score :{}".format(linear_model.score(X_train_scaled, y_train)))
print("test score :{}".format(linear_model.score(X_test_scaled, y_test)))

plt.scatter(X_test, y_test, label='Data (Test Set)', color='green')
plt.plot(X_test, y_pred, label='Linear Regression Model', color='orange')
plt.title('California Housing: Median Income vs House Value')
plt.xlabel('Median Income (MedInc)')
plt.ylabel('House Value')
plt.legend()
plt.show()

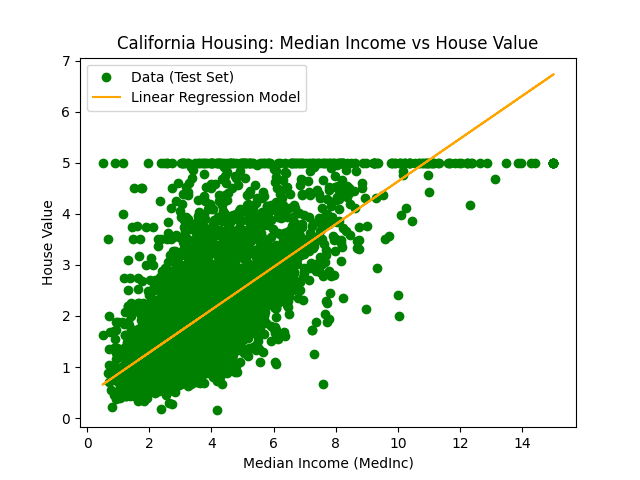
オレンジ色の線が線形回帰モデルで、元のデータから収入と家賃の散布図を作成し、1つの特徴量（Median Income）を学習モデルをフィッティングしています。

線形モデルは（もちろん）線形なので、California housingのような分散したデータに合わせるとデータの特徴を削ぎ落したかなり無理やりなモデルに見えます。

train score :0.47577303714678176
test score :0.467736963670335

トレーニングデータでのスコアとテストデータでのスコアが近いので、適合不足の可能性があります。一般に線形モデルは高次元データに対して良く機能するので、特徴量が８つしかないCarifornia housingデータセットからさらに次元を落としたデータでは本領を発揮できないのでしょうか。

次は8つの特徴量をすべて使ってモデルを構築し、そのモデルが返したテストデータでの予測結果をプロットしてみたいと思います。

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

data = fetch_california_housing()
X = data.data
y = data.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

linear_model = LinearRegression()
linear_model.fit(X_train_scaled, y_train)

y_pred = linear_model.predict(X_test_scaled)

print("train score :{}".format(linear_model.score(X_train_scaled, y_train)))
print("test score :{}".format(linear_model.score(X_test_scaled, y_test)))

feature_names = data.feature_names
plt.figure(figsize=(20, 15))

for i in range(X.shape[1]):
    plt.subplot(3, 3, i + 1)
    plt.scatter(X_test[:, i], y_test, label='Data (Test Set)', color='green', alpha=0.5)
    plt.scatter(X_test[:, i], y_pred, label='Predictions', color='orange', alpha=0.5)
    plt.title(f'{feature_names[i]} vs House Value')
    plt.xlabel(feature_names[i])
    plt.ylabel('House Value')
    plt.legend()

plt.tight_layout()
plt.show()
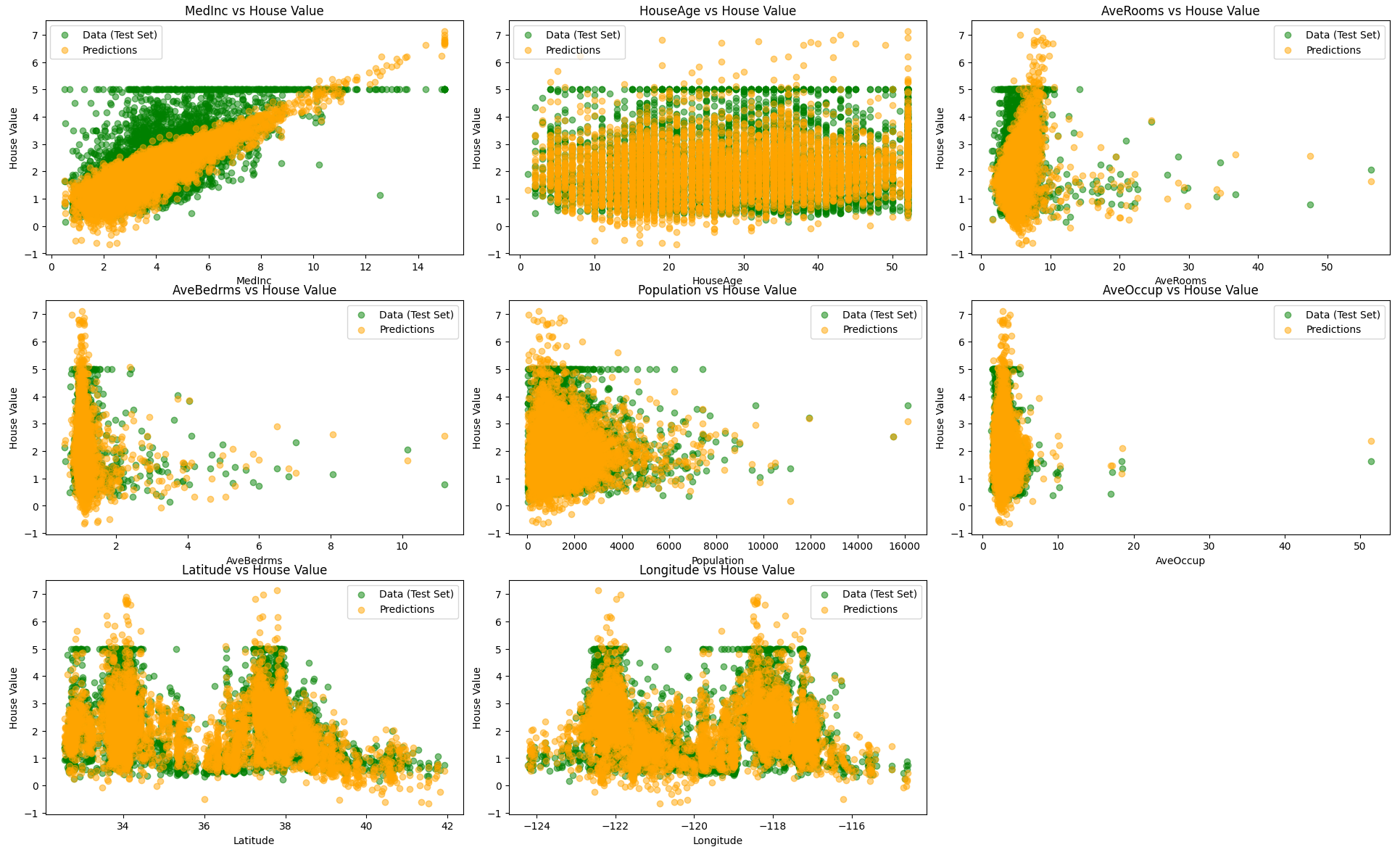
train score :0.6063839594000304
test score :0.6053413843268582

かなり改善しました。やはりデータの次元は高い方が相性がいいということが分かりました。しかし、スコアはそれほど良いとは言えず、これでもまだまだ適合不足に見えます。

他のモデルではどうなのでしょうか？

■リッジ回帰

リッジ回帰は線形回帰の一種で、w（モデルの係数）の二乗和にペナルティを課してモデルが複雑になること（過剰適合）を防ぐアルゴリズムです。

これはL2正規化と呼ばれ、下記の損失関数を用います。

$$ F_{loss} = ||y\ -\ Xw||_2^2 \ +\ \alpha||w||_2^2 $$

第一項がモデルの予測誤差の二乗和で、第二項が正規化項で係数wの二乗和に比例するペナルティを表しています。
前についている係数αは正規化の強さを制御するパラメータで、これを小さくすると係数へのペナルティは小さくなり、大きくすると係数へのペナルティが大きくなります。
ペナルティを非常に小さくしていくと係数への制約がほとんどなくなり線形回帰のようになります。

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

data = fetch_california_housing()
X = data.data
y = data.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

linear_model = Ridge(alpha=1.0)
linear_model.fit(X_train_scaled, y_train)

y_pred = linear_model.predict(X_test_scaled)

print("train score :{}".format(linear_model.score(X_train_scaled, y_train)))
print("test score :{}".format(linear_model.score(X_test_scaled, y_test)))

feature_names = data.feature_names
plt.figure(figsize=(20, 15))

for i in range(X.shape[1]):
    plt.subplot(3, 3, i + 1)
    plt.scatter(X_test[:, i], y_test, label='Data (Test Set)', color='green', alpha=0.5)
    plt.scatter(X_test[:, i], y_pred, label='Predictions', color='orange', alpha=0.5)
    plt.title(f'{feature_names[i]} vs House Value')
    plt.xlabel(feature_names[i])
    plt.ylabel('House Value')
    plt.legend()

plt.tight_layout()
plt.show()
train score :0.606383872154561
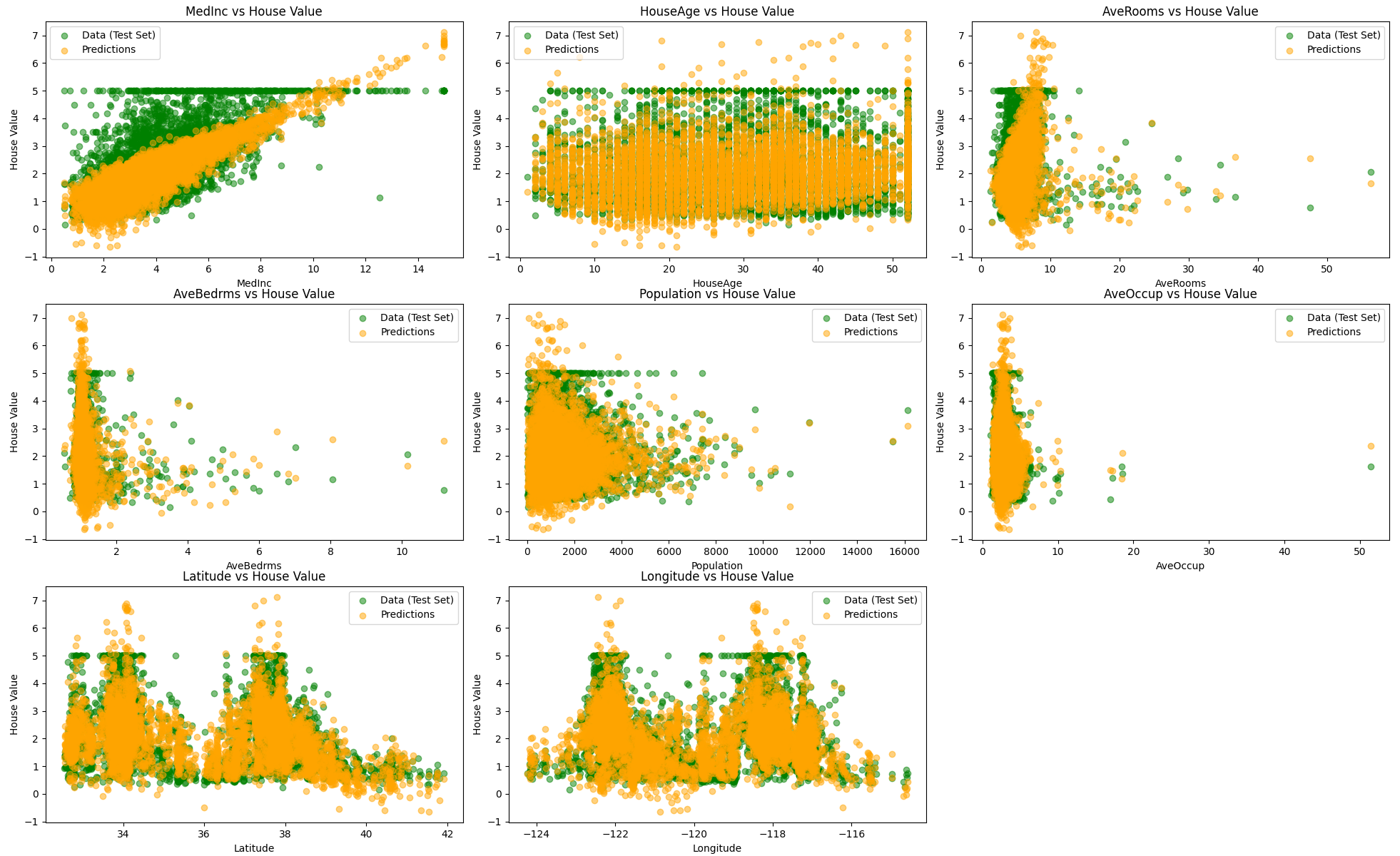
test score :0.6053284706740671

デフォルトの設定では性能はほとんど変わりませんでした。元々過剰適合ではなく寧ろ適合不足だったのでリッジ回帰の良さが出なかったのかもしれませんし、データの次元が低すぎたのかもしれません。

■Lasso

最後にLasso回帰（Least Absolute Shrinkage and Selection Operator）を試してみます。

このモデルはリッジ回帰と同様に線形回帰に制約をかけるのですが、L2正規化を用いていたリッジ回帰と違い、L1正規化を使います。

$$ min \displaystyle \sum_{i=1}^N (y_i \ -\ \hat{y_i})^2 + \alpha \displaystyle \sum_{j=1}^p |w_j| $$

L1正規化は係数の絶対値の和にペナルティを課すので、いくつかの係数が完全に0になります。つまり特徴量を自動的に選択していくという挙動をします。

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

data = fetch_california_housing()
X = data.data
y = data.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

lasso_model = Lasso(alpha=0.1, max_iter=100000)
lasso_model.fit(X_train_scaled, y_train)

y_pred = lasso_model.predict(X_test_scaled)

print("train score :{}".format(lasso_model.score(X_train_scaled, y_train)))
print("test score :{}".format(lasso_model.score(X_test_scaled, y_test)))

feature_names = data.feature_names
plt.figure(figsize=(20, 15))

for i in range(X.shape[1]):
    plt.subplot(3, 3, i + 1)
    plt.scatter(X_test[:, i], y_test, label='Data (Test Set)', color='green', alpha=0.5)
    plt.scatter(X_test[:, i], y_pred, label='Predictions', color='orange', alpha=0.5)
    plt.title(f'{feature_names[i]} vs House Value')
    plt.xlabel(feature_names[i])
    plt.ylabel('House Value')
    plt.legend()

plt.tight_layout()
plt.show()
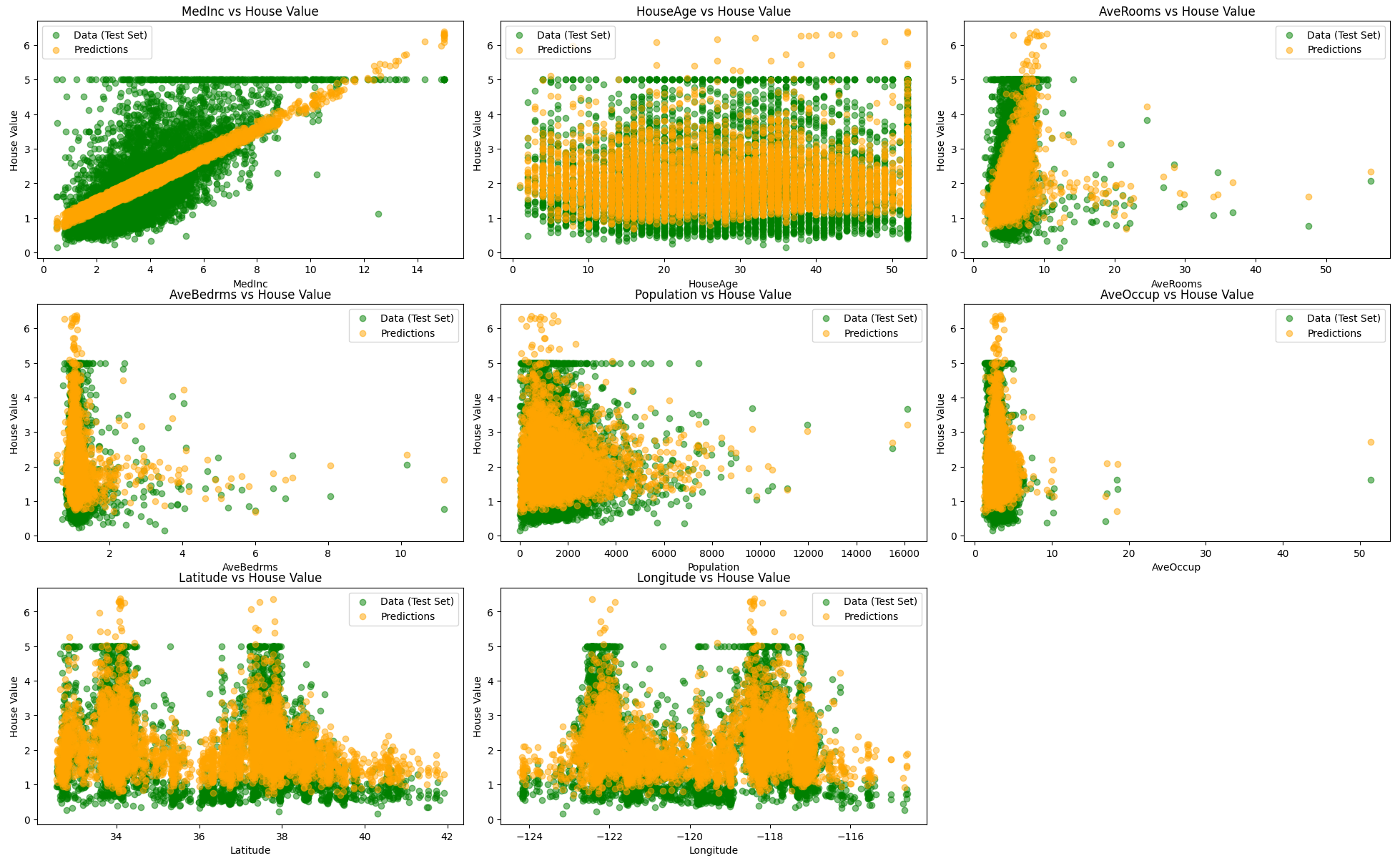
train score :0.4979225576753856
test score :0.4853577696946444

次元が落ちている様子がグラフから確認できますが、元々低次元データセットなのであまり恩恵はないみたいです。（ちなみにα=0.01くらいに調整するとリッジ回帰と同等のスコアにはなります。）

もう一度（標準化された）データを見てみると、外れ値と思われるプロットが散見されます。


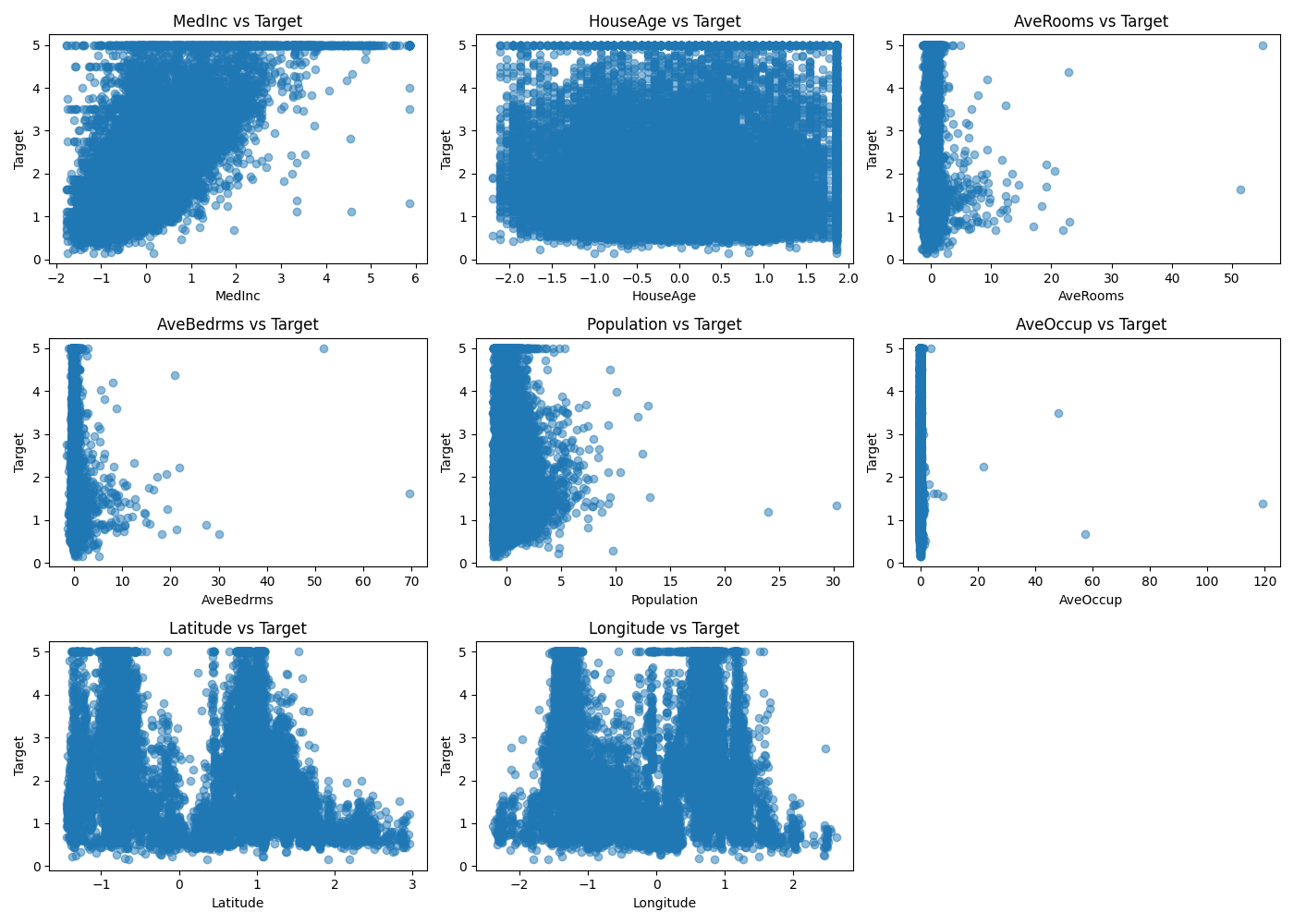
線形モデルによる予測結果を見てみるとどうやらこの値に引っ張られて外れ値（と想像する値）を予測してしまっています。学習させる前にもっと事前処理が必要だったことが分かりました。

線形回帰の予測結果

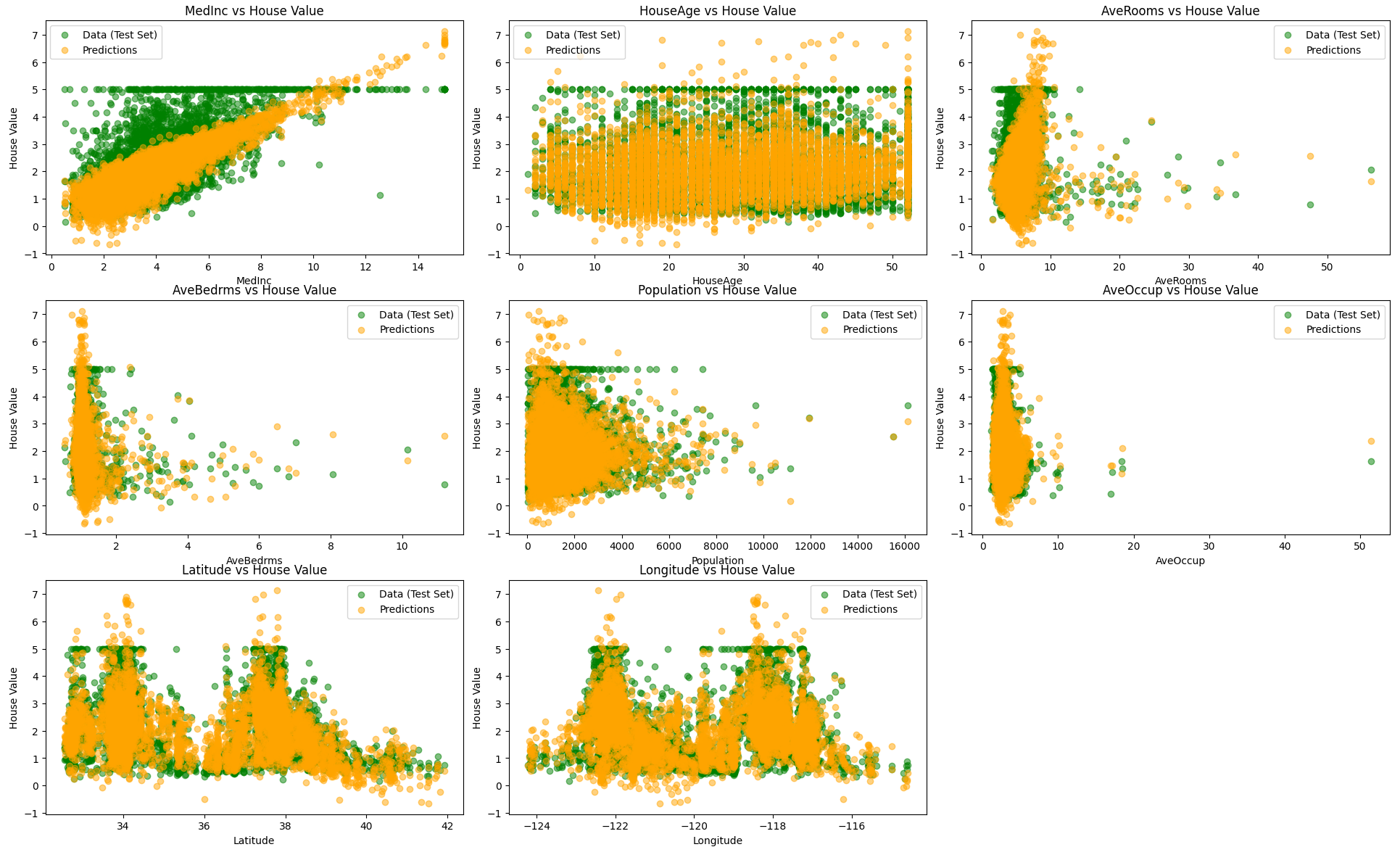
■おわりに

今回は良さげな標準データセット（データ数が多くて整っている高次元データセット）が見つからなかったので、California housing データセットに突っ込んでみましたが、思いの他良いスコアを出すことが難しかったです。
またいつかデータを整えてリベンジしたいと思います。

■参考文献

  1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
  2. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
  3. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html

hammertime

, ,
, , , ,

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です