AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day9
経緯についてはこちらをご参照ください。
■本日の進捗
●k-最近傍法を使えるようになる
■k-NNを様々なデータセットで試してみた
前回の 最も単純な機械学習アルゴリズム 「怠惰学習」 ではk-NNを、あやめデータセットとCalifornia housingデータセットに適用し、k値の最適化を実施してみました。
今回はこれらのデータセットに加えてそれ以外のscikit-learn標準データセットを用いて、k-NNの挙動を見ていきたいと思います。
それでは最初に、前回も用いたあやめ(iris)データセットで遊んでみます。
ユークリッド距離を用いた場合のk値の最適解を求めていきますが、前回と違いもっと単純な評価関数(score関数)で解析をしてみます。(そろそろPowerShell直書きが厳しくなってきたので愛用のVSCodeでやっていきます)
Iris dataset(例:ユークリッド距離の場合)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
data = load_iris()
X = data.data
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
mean_scores = []
for k in k_range:
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X_train, y_train)
scores = model.score(X_test, y_test)
mean_scores.append(scores)
optimal_k = k_range[np.argmax(mean_scores)]
print(f'Optimal k: {optimal_k}')
print(f"score: {mean_scores[optimal_k]}")
plt.figure(figsize=(10, 6))
plt.plot(k_range, mean_scores, marker='o', linestyle='-', label='Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN: Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
Iris dataset(例:マンハッタン距離の場合)
model = KNeighborsClassifier(n_neighbors=k, metric='manhattan')
Iris dataset 結果
ユークリッド距離
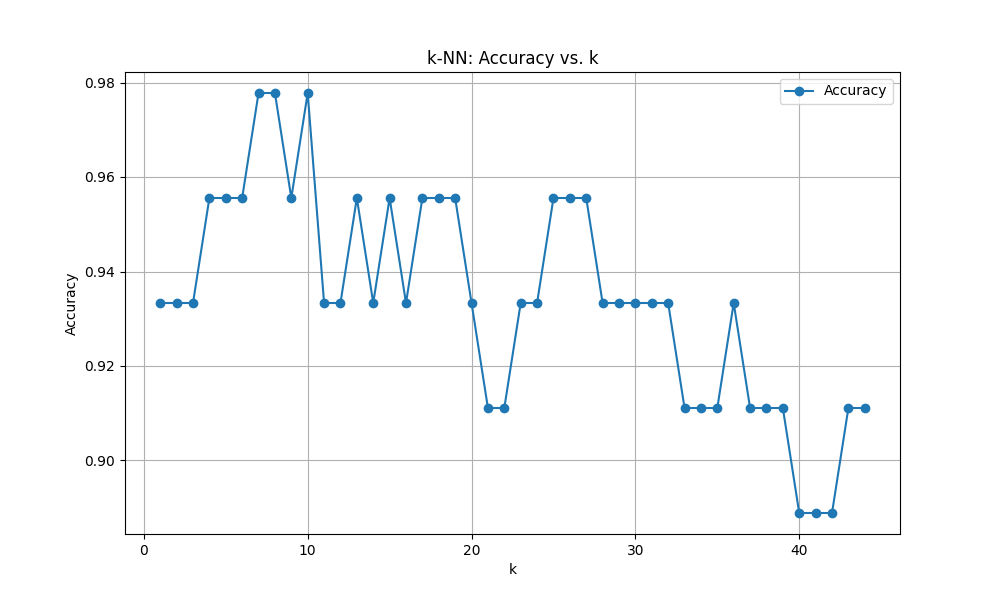
Optimal k: 7
score: 0.9777777777777777
マンハッタン距離

Optimal k: 13
score: 0.9555555555555556
前回の結果と比較すると評価関数が変わっているので若干の違いはあるものの、ユークリッド距離の方がスコアは高いです。
一般的にユークリッド距離は低次元で連続的な特徴量が得意で、マンハッタン距離は各軸ごとに離散的な特徴量で高次元な場合でも機能すると言われています。そう考えるとあやめ(Iris)データセットは(花びらの幅や長さ等)連続値で特徴量4つの低次元データセットなので、ユークリッド距離と相性が良いのは理解ができます。(マンハッタン距離と相性が悪いとは言っていない)
同様のWineデータセットでも見てみようと思います。
このデータセットは、3つの品種を13の特徴量で振り分けたもので、酸濃度など化学的な連続値の低次元データセットです。(特徴量13は多そうに見えますが、一応アルゴリズム的には低次元です。)
Wine dataset(例:ユークリッド距離の場合)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
data = load_wine()
X = data.data
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
mean_scores = []
for k in k_range:
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X_train, y_train)
scores = model.score(X_test, y_test)
mean_scores.append(scores)
optimal_k = k_range[np.argmax(mean_scores)]
print(f'Optimal k: {optimal_k}')
print(f"score: {mean_scores[optimal_k]}")
plt.figure(figsize=(10, 6))
plt.plot(k_range, mean_scores, marker='o', linestyle='-', label='Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN: Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
Wine dataset 結果
ユークリッド距離
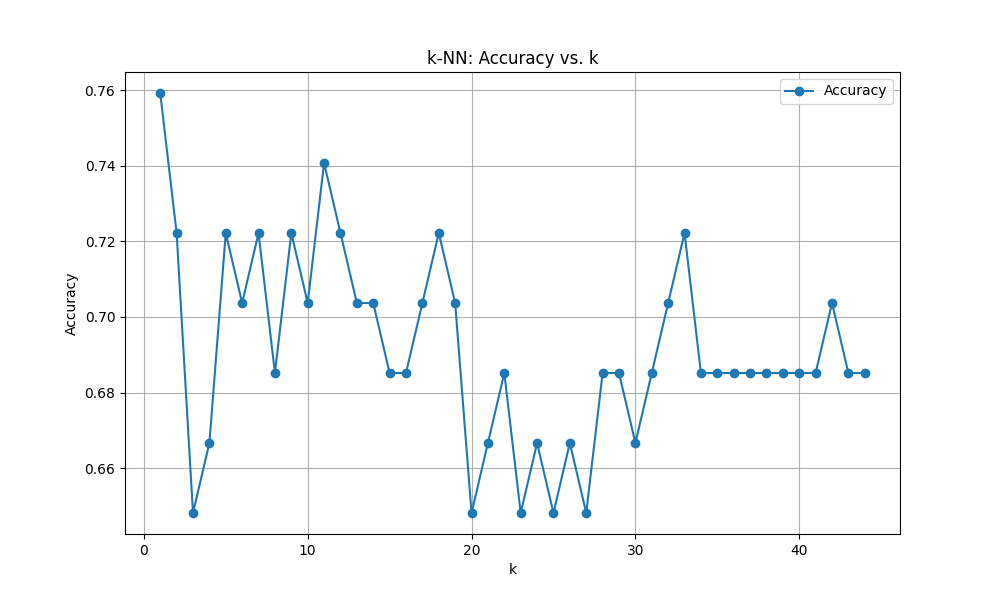
Optimal k: 1
score: 0.7222222222222222
マンハッタン距離
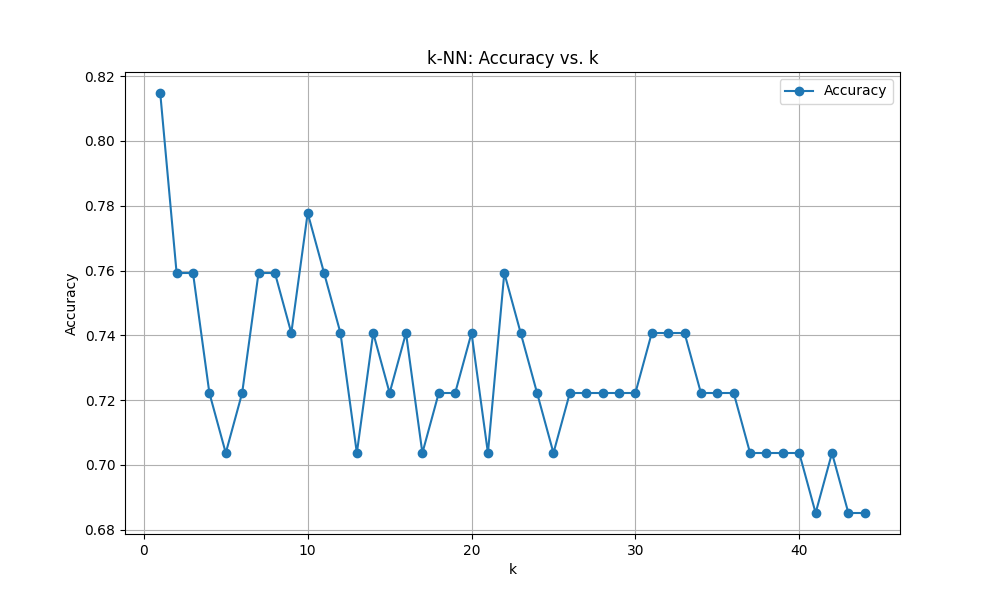
Optimal k: 1
score: 0.7592592592592593
結果はマンハッタン距離の方が優れていました。これは当初の予想とは異なります。連続値で低次元なデータセットにはユークリッド距離でも十分精度が出るはずです。
ここで、Wineデータセットの中身を見てみたいと思います。
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
data = load_wine()
df = pd.DataFrame(data.data, columns=data.feature_names)
n_features = df.shape[1]
fig, axes = plt.subplots(nrows=(n_features + 2) // 3, ncols=3, figsize=(15, 12))
for i, ax in enumerate(axes.flatten()):
if i < len(df.columns):
ax.hist(df.iloc[:, i], bins=20, alpha=0.7, color='blue', label='Original')
ax.set_title(df.columns[i])
else:
ax.axis('off')
plt.tight_layout()
plt.show()
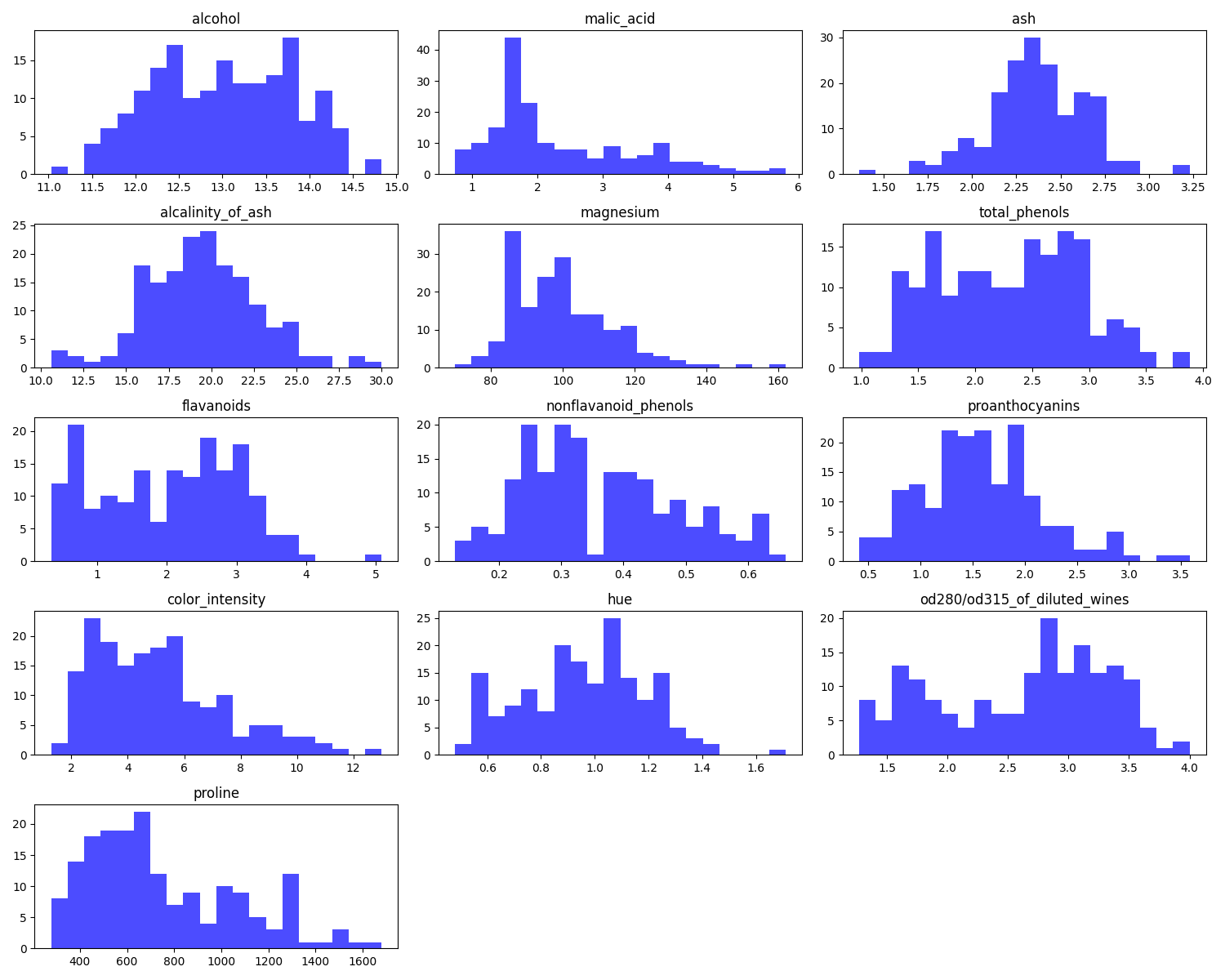
nonflavanoid_phenols(非フラバノイドフェノール類)は横軸を0.2~0.6辺りに集中していますが、proline(プロリン、これらはワインに含まれる化学物質なのだと思います。おそらく。)は400~500辺りに多く、1600にまで及んでいます。スケールが不均一なのでしょうか。標準化と呼ばれる平均を0に、標準偏差を1にするStandardScalerを使ってスケーリングしてみます。
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
data = load_wine()
df = pd.DataFrame(data.data, columns=data.feature_names)
scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)
scaled_df = pd.DataFrame(scaled_data, columns=data.feature_names)
n_features = scaled_df.shape[1]
fig, axes = plt.subplots(nrows=(n_features + 2) // 3, ncols=3, figsize=(15, 12))
for i, ax in enumerate(axes.flatten()):
if i < len(df.columns):
ax.hist(scaled_df.iloc[:, i], bins=20, alpha=0.7, color='blue', label='Original')
ax.set_title(scaled_df.columns[i])
else:
ax.axis('off')
plt.tight_layout()
plt.show()
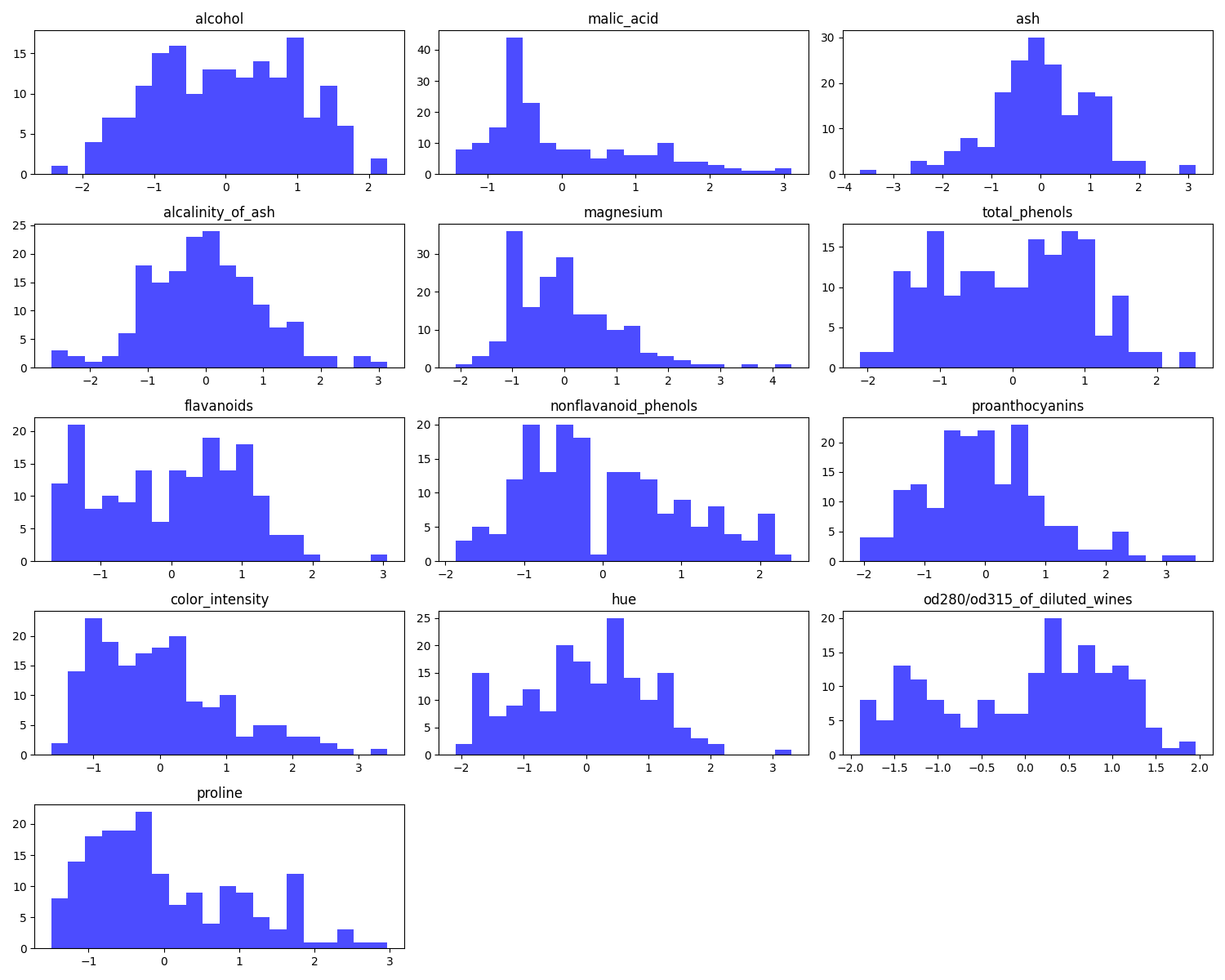
スケーリングできました。すべての特徴量同士で値の乖離が解消されました。これでユークリッド距離のみならず、マンハッタン距離も精度が上がるでしょう。試してみます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
data = load_wine()
scaler = StandardScaler()
df = pd.DataFrame(data.data, columns=data.feature_names)
scaled_data = scaler.fit_transform(df)
df_scaled = pd.DataFrame(scaled_data, columns=data.feature_names)
X = df_scaled
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
mean_scores = []
for k in k_range:
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X_train, y_train)
scores = model.score(X_test, y_test)
mean_scores.append(scores)
optimal_k = k_range[np.argmax(mean_scores)]
print(f'Optimal k: {optimal_k}')
print(f"score: {mean_scores[optimal_k]}")
plt.figure(figsize=(10, 6))
plt.plot(k_range, mean_scores, marker='o', linestyle='-', label='Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN: Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
ユークリッド距離
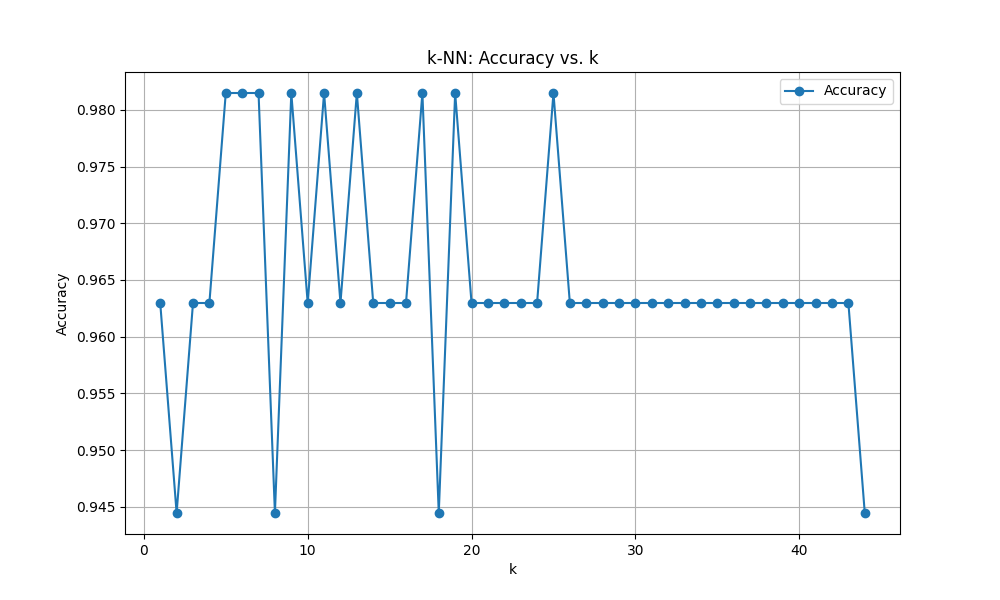
Optimal k: 5
score: 0.9814814814814815
マンハッタン距離
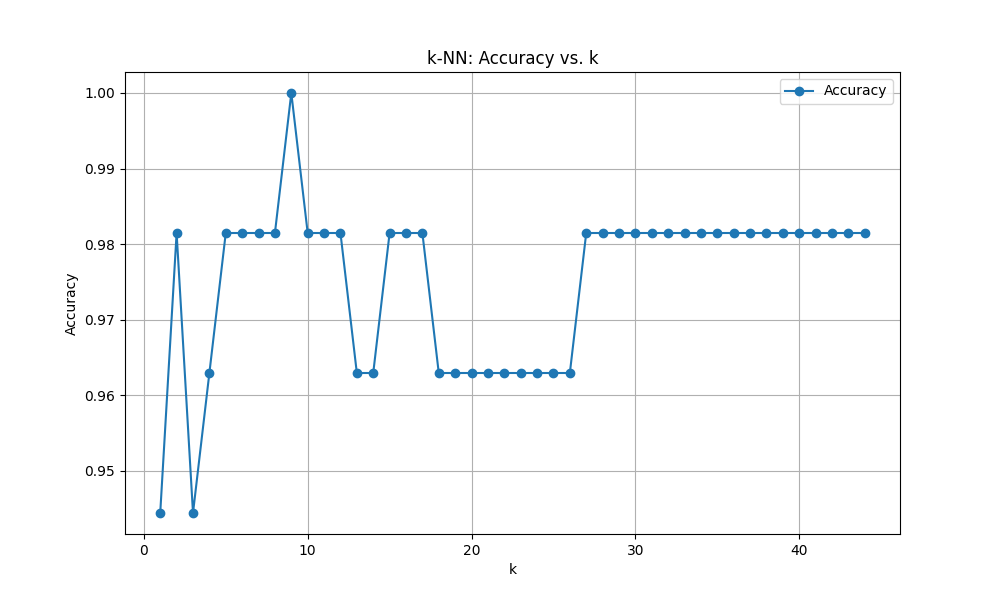
Optimal k: 9
score: 0.9814814814814815
スケーリング様様です。ユークリッド距離もマンハッタン距離もとんでもないスコアを叩き出しました。しかしこれは過剰適合(オーバーフィッティング)の可能性もあります。
過剰適合かどうか、テストデータに対しても解析していき、改めてk値の最適解を検討してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
data = load_wine()
scaler = StandardScaler()
df = pd.DataFrame(data.data, columns=data.feature_names)
scaled_data = scaler.fit_transform(df)
df_scaled = pd.DataFrame(scaled_data, columns=data.feature_names)
X = df_scaled
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
train_scores = []
test_scores = []
for k in k_range:
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
train_scores.append(train_score)
test_score = model.score(X_test, y_test)
test_scores.append(test_score)
optimal_k = k_range[np.argmax(test_scores)]
print(f'Optimal k: {optimal_k}')
print(f"Best Test Score: {test_scores[np.argmax(test_scores)]}")
plt.figure(figsize=(12, 6))
plt.plot(k_range, train_scores, marker='o', linestyle='-', color='orange', label='Training Accuracy')
plt.plot(k_range, test_scores, marker='o', linestyle='-', color='g', label='Test Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN: Training and Test Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
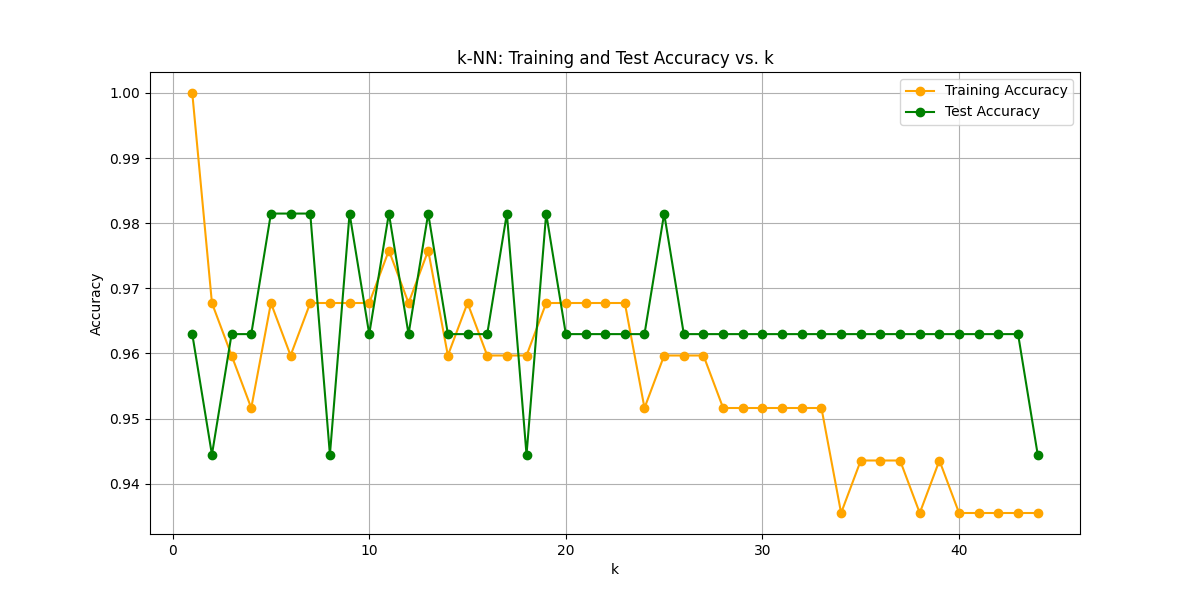
k=1はトレーニングデータでの精度が1.0を示していて明らかに過剰適合(というより自分自身の値そのもの)ですが、それ以降はk=20を過ぎたあたりまでほとんど変化がありません。恐らく先ほどの最適解k=5(ユークリッド距離の場合)はかなり良いモデルだったことが分かりました。
もちろん前処理や評価指標などまだまだ改善の余地はあるかと思いますが、「Pythonではじめる機械学習」40ページ目の初学者にはこの辺が限界でしょうか。
■おわりに
今回のすべての例で正規化や次元削減は行っていません。それでもこれだけ雑に使ってそれなりの結果を返してくれているのは、(もちろん標準データセットが綺麗なのもあるだろうけども)k-NNのメリットではないでしょうか。何も調整せずにここまで合うのであれば、アプリケーションによっては即日実装できそうな勢いです。まさに実装しやすく理解しやすいk-NNアルゴリズムの良さを体感できました。
k-NN楽しい!!!
どんどん先に進んでいきたいのですが、あまりに楽しいのでもう一回くらいk-NNやらせてください…
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- k近傍法アルゴリズムとは. ibm.com. https://www.ibm.com/jp-ja/topics/knn
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html