最も単純な機械学習アルゴリズム 「怠惰学習」

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day8

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

●k-最近傍法を理解

■いちばんはじめの機械学習

昨日までで「Pythonではじめる機械学習（オライリー・ジャパン）」の導入に載っているライブラリ（scikit-learn以外）はすべて浅く理解ができました。今日からはscikit-learnをベースに、いよいよ機械学習に入っていきます。
まずは最初のモデル：k-最近傍法を見ていきます。

●k-最近傍法（k-NN：k-Nearest Neighbors）

k-NNは新しいデータポイントを分類したり予測する際に、予め与えられたデータポイントの中で最も近い（様々な測定方法があるが、”距離的に” 近い）k個のデータポイントを基にして答えを導き出すアルゴリズムです。

その歴史は古く、パターン認識や統計における考え方「近傍点を用いた分類」を起源と考えられており、1960年代には既にこれに近いアルゴリズムが研究されていました。1970年代になると一気に研究が進み、機械学習やパターン認識に関するアルゴリズムとして理論的にもその立場が確立されました。1980年代以降、さらに一般にも広く普及し実際のアプリケーションにも多く利用されるようになりました。現在でも大規模データや高次元データに対する研究が行われ、最も単純なアルゴリズムでありながら広く実用されています。

●データポイント間の距離を求める

あるデータポイントとデータポイント（点と点）がどのくらい離れているのか、近いのか？遠いのか？を知るためには距離を測らなくてはいけません。

ミンコフスキー距離

$$ d(P, Q) = (\sum_{i=1}^{n} \begin{vmatrix} x_{i} – y_{i} \end{vmatrix})^{1/p} $$

p=2の時にはユークリッド距離と呼ばれ、k-NNでも最も一般的に使われる距離指標になります。平面上または空間上での2点間の最短直線距離を示します。各次元が同じスケールの場合によく機能するものの、高次元空間には向かないです。その代わりに最も理解しやすいのがメリットでもあります。

p=1の時にはマンハッタン距離と呼ばれ、その名の通り（京都のような、マンハッタンもそうなの？知らんけど。碁盤状の）市街地の道路を通ってある点からある点を移動する距離を考えるとわかりやすいかもしれません。これは2点間を軸に沿って直角に移動する時の総移動距離を返すことから付けられた名前です。
このことから異なるスケールのデータでも良く機能し、ノイズに対しても、高次元データに対しても比較的強いです。

●侮るなかれ、割と万能型なk-NN

k-NNはクラス分類にも回帰にも使える優秀な子です。

クラス分類（不連続値）の場合は、新しいデータポイントが予め与えられたデータポイントの中で最も近いk点（もちろん1点でもいいし、その方が理解しやすいかもしれない）の多数決を取り、そのデータポイントと同じクラス（仲間）に分類されます。
例えば、山で見つけた植物がどんな種類の植物なのかをその特徴（茎の太さ、長さ、花弁の幅、長さ、枚数…等）から類推することができます。

回帰（連続値）の場合には、k個の最も近いデータポイントの中で平均値を取り、その値を予測結果として返します。
例えば、近隣の住宅や土地の価格から新しい住宅の価格を推定することができます。

●教師がいるのに勉強しない子？

k-NNは教師あり学習（ラベル付きのデータを使うアルゴリズム）に分類されるのですが、遅延学習（怠惰学習）と呼ばれるモデルの一種で、一般的な機械学習の「学習段階（トレーニング）」では何も学習していません。あくまでデータセットを保存するだけで、実際に予測を行う際にそのデータセットを参照しながら計算を行い結果を返しています。

●k値の最適化

k-NNのハイパーパラメータはkと距離のみなので、k値を最適化しようと思います。

k値の最適化には1から44の範囲で繰り返しモデルを作って予測を繰り返し、その結果スコアが最も高かったk値を最適解とする方法を使ってみます。（要は総当たりです。）この時のスコアにはCVスコアというものが良いらしいのですが、今のところ良くわかってないです。ただ、「Pythonではじめる機械学習」には第5章に言及があるのでそこまで楽しみにしたいと思います。（本当はそろそろ寝ないと死にそうなだけです…）

まずは上記の本でも適用している、irisデータセット（あやめの花：setosa, versicolor, virginica のガクの長さ、ガクの幅、花弁の長さ、花弁の幅）を用いてパラスタしていきます。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split, cross_val_score
>>> from sklearn.neighbors import KNeighborsClassifier
>>>
>>> data = load_iris()
>>> X = data.data
>>> y = data.target
>>>
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
>>>
>>> k_range = range(1, 45)
>>> cv_scores = []
>>>
>>> for k in k_range:
...     model = KNeighborsClassifier(n_neighbors=k)
...     scores = cross_val_score(model, X_train, y_train, cv=10, scoring='accuracy')
...     cv_scores.append(scores.mean())
...
>>>
>>> optimal_k = k_range[np.argmax(cv_scores)]
>>> print(f'Optimal k: {optimal_k}')
Optimal k: 3
>>> print(f'score: {max(cv_scores):.2f}')
score: 0.98
>>>
>>> plt.figure(figsize=(10, 6))
<Figure size 1000x600 with 0 Axes>
>>> plt.plot(k_range, cv_scores, marker='o', label='Cross-Validation Accuracy')
[<matplotlib.lines.Line2D object at 0x000001F3861B0D40>]
>>> plt.xlabel('k')
Text(0.5, 0, 'k')
>>> plt.ylabel('Cross-Validation Accuracy')
Text(0, 0.5, 'Cross-Validation Accuracy')
>>> plt.title('k-NN: Accuracy vs. k')
Text(0.5, 1.0, 'k-NN: Accuracy vs. k')
>>> plt.legend()
<matplotlib.legend.Legend object at 0x000001F384FB4B00>
>>> plt.grid(True)
>>> plt.show()

最適解はk=3、CVスコアは0.98でした。良い結果に見えますが、モデルとして良いかどうかは別の話です。（ここでは言及しません）

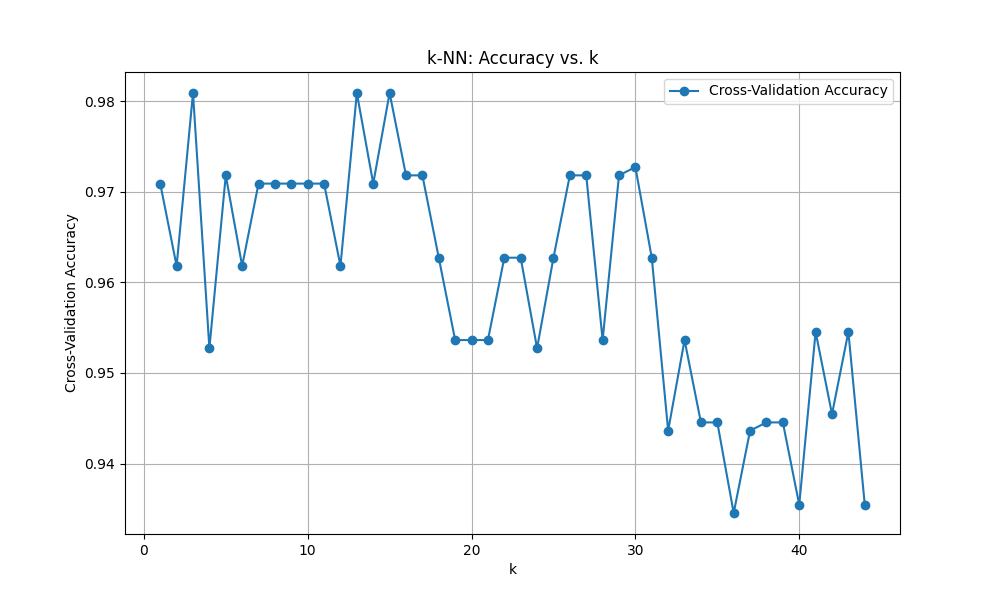
ちなみにirisデータセットのサンプル数は150でした。

>>> data = load_iris()
>>> print("data: {}".format(data['data'].shape))
data: (150, 4)

もう少し大きなデータセットにも適用してみたいと思います。これもscikit-learnの標準データセットにあるcalifornia housingデータセット（カリフォルニアの世帯収入、築年数、1住宅当たりの平均部屋数、平均寝室数、人口、1住宅当たりの平均居住者数、緯度、経度）です。先ほどのirisデータセットよりサンプル数が増えますが、k値の推移はどう変化していくのでしょうか。

>>> import numpy as np
>>> from sklearn.datasets import fetch_california_housing
>>> from sklearn.model_selection import train_test_split, cross_val_score
>>> from sklearn.neighbors import KNeighborsClassifier
>>> import matplotlib.pyplot as plt
>>>
>>> data = fetch_california_housing()
>>> X = data.data
>>> y = data.target
>>>
>>> median_price = np.median(y)
>>> y_class = (y > median_price).astype(int)  # class1 is higher
>>>
>>> X_train, X_test, y_train, y_test = train_test_split(X, y_class, test_size=0.3, random_state=8)
>>>
>>> k_range = range(1, 45)
>>> mean_scores = []
>>>
>>> for k in k_range:
...     model = KNeighborsClassifier(n_neighbors=k)
...     scores = cross_val_score(model, X_train, y_train, cv=10, scoring='accuracy')
...     mean_scores.append(scores.mean())
...
>>> best_k = k_range[np.argmax(mean_scores)]
>>> best_score = max(mean_scores)
>>>
>>> print(f"Optimal k: {best_k}")
Optimal k: 5
>>> print(f"score: {best_score:.2f}")
score: 0.61
>>>
>>> plt.figure(figsize=(10, 6))
<Figure size 1000x600 with 0 Axes>
>>> plt.plot(k_range, mean_scores, marker='o')
[<matplotlib.lines.Line2D object at 0x000001F384FBC650>]
>>> plt.title('Optimal k for k-NN (Cross-Validation)')
Text(0.5, 1.0, 'Optimal k for k-NN (Cross-Validation)')
>>> plt.xlabel('k Value')
Text(0.5, 0, 'k Value')
>>> plt.ylabel('Accuracy (Mean Cross-Validation Score)')
Text(0, 0.5, 'Accuracy (Mean Cross-Validation Score)')
>>> plt.xticks(k_range)
([<matplotlib.axis.XTick object at 0x000001F384FB4A10>, <matplotlib.axis.XTick object at 0x000001F384FB4230>, <matplotlib.axis.XTick object at 0x000001F384FA2DB0>, <matplotlib.axis.XTick object at 0x000001F384FBCF20>, <matplotlib.axis.XTick object at 0x000001F384FBD8B0>, <matplotlib.axis.XTick object at 0x000001F384FBDF40>, <matplotlib.axis.XTick object at 0x000001F384FBEC00>, <matplotlib.axis.XTick object at 0x000001F384FBF590>, <matplotlib.axis.XTick object at 0x000001F384FBEFF0>, <matplotlib.axis.XTick object at 0x000001F384FBFD70>, <matplotlib.axis.XTick object at 0x000001F384FC46B0>, <matplotlib.axis.XTick object at 0x000001F384FC5010>, <matplotlib.axis.XTick object at 0x000001F384FC59A0>, <matplotlib.axis.XTick object at 0x000001F384FC6330>, <matplotlib.axis.XTick object at 0x000001F384FC4D10>, <matplotlib.axis.XTick object at 0x000001F384FC6A20>, <matplotlib.axis.XTick object at 0x000001F384FC73E0>, <matplotlib.axis.XTick object at 0x000001F384FC7D10>, <matplotlib.axis.XTick object at 0x000001F384FC8830>, <matplotlib.axis.XTick object at 0x000001F384FC6DB0>, <matplotlib.axis.XTick object at 0x000001F384E39430>, <matplotlib.axis.XTick object at 0x000001F384E39DF0>, <matplotlib.axis.XTick object at 0x000001F384E3A7B0>, <matplotlib.axis.XTick object at 0x000001F384E3B140>, <matplotlib.axis.XTick object at 0x000001F384FC4860>, <matplotlib.axis.XTick object at 0x000001F384DBA300>, <matplotlib.axis.XTick object at 0x000001F384FB29F0>, <matplotlib.axis.XTick object at 0x000001F384E3B890>, <matplotlib.axis.XTick object at 0x000001F3871B41A0>, <matplotlib.axis.XTick object at 0x000001F3871B4B60>, <matplotlib.axis.XTick object at 0x000001F384D6F590>, <matplotlib.axis.XTick object at 0x000001F3871B5160>, <matplotlib.axis.XTick object at 0x000001F3871B5A90>, <matplotlib.axis.XTick object at 0x000001F3871B6420>, <matplotlib.axis.XTick object at 0x000001F3871B6DB0>, <matplotlib.axis.XTick object at 0x000001F3871B6810>, <matplotlib.axis.XTick object at 0x000001F3871B74D0>, <matplotlib.axis.XTick object at 0x000001F3871B7E30>, <matplotlib.axis.XTick object at 0x000001F3871D07A0>, <matplotlib.axis.XTick object at 0x000001F3871D1130>, <matplotlib.axis.XTick object at 0x000001F3871B5D60>, <matplotlib.axis.XTick object at 0x000001F3871D1850>, <matplotlib.axis.XTick object at 0x000001F3871D2180>, <matplotlib.axis.XTick object at 0x000001F3871D2AB0>], [Text(1, 0, '1'), Text(2, 0, '2'), Text(3, 0, '3'), Text(4, 0, '4'), Text(5, 0, '5'), Text(6, 0, '6'), Text(7, 0, '7'), Text(8, 0, '8'), Text(9, 0, '9'), Text(10, 0, '10'), Text(11, 0, '11'), Text(12, 0, '12'), Text(13, 0, '13'), Text(14, 0, '14'), Text(15, 0, '15'), Text(16, 0, '16'), Text(17, 0, '17'), Text(18, 0, '18'), Text(19, 0, '19'), Text(20, 0, '20'), Text(21, 0, '21'), Text(22, 0, '22'), Text(23, 0, '23'), Text(24, 0, '24'), Text(25, 0, '25'), Text(26, 0, '26'), Text(27, 0, '27'), Text(28, 0, '28'), Text(29, 0, '29'), Text(30, 0, '30'), Text(31, 0, '31'), Text(32, 0, '32'), Text(33, 0, '33'), Text(34, 0, '34'), Text(35, 0, '35'), Text(36, 0, '36'), Text(37, 0, '37'), Text(38, 0, '38'), Text(39, 0, '39'), Text(40, 0, '40'), Text(41, 0, '41'), Text(42, 0, '42'), Text(43, 0, '43'), Text(44, 0, '44')])
>>> plt.grid(True)
>>> plt.show()

最適解はk=6、CVスコアは0.61でした。

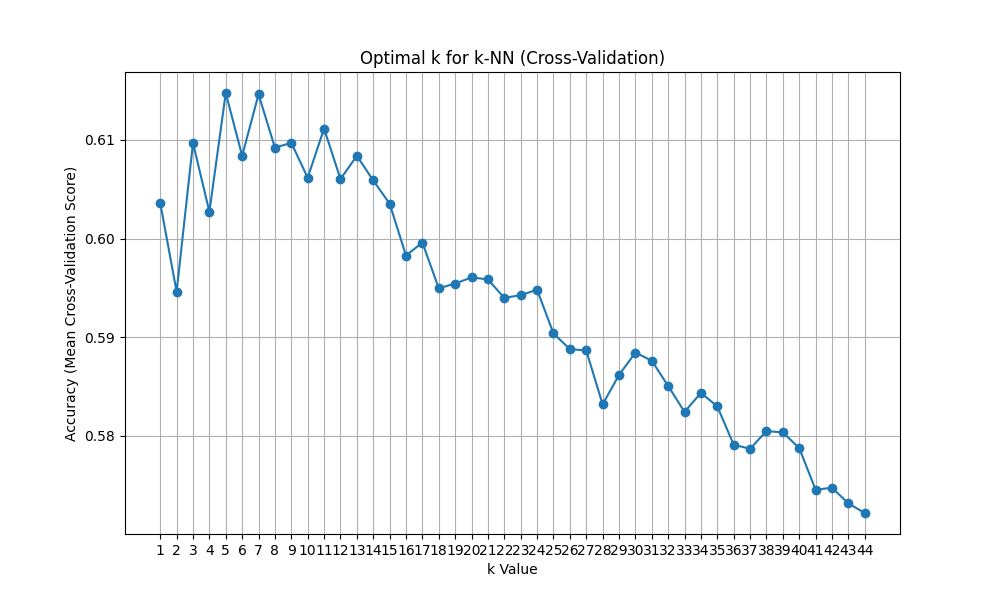
ちなみにサンプル数は20640です。

>>> data = fetch_california_housing()
>>> print("data: {}".format(data['data'].shape))
data: (20640, 8)

うーん、スコアがすこぶる悪いです。本来はある程度スコアを上げてからk値を最適化するのではと推測しますが、それはまた今度勉強していきたいと思います。

ただ、このデータからも重要なことがわかります。k値の値を増やすと遠くのデータも参照していくことにあるので、ノイズ（この標準データセットはかなり綺麗に整えられたデータですが）や類似性の低いデータまで同じクラスとして分類してしまう可能性があります。なのでk＝1の精度がそれほど良くないのが直観的であるのと同じく、k値を増やせば増やすほど精度が落ちていくのも予想通りの結果となりました。k-NNはハイパーパラメータが少ないだけにk値の最適化は精度に対する寄与度がとても高いのだと思います。

■おわりに

今日は初めてk-NNに触れました。本当は1日でこの項目を終えるつもりでしたが、モデル精度に関してまでは触れられなかったので、明日は他のデータセットも使ってもう少しk-NNに触れていきたいと思います。

■参考文献

1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
2. k近傍法アルゴリズムとは. ibm.com. https://www.ibm.com/jp-ja/topics/knn
3. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
4. Christopher M. Bishop. Pattern Recognition and Machine Learning. Springer. 2006. 798p.
5. R. James, G., Witten, D., Hastie, T., Tibshirani. An Introduction to Statistical Learning. Springer. 2013. 426p.
6. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html