AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day66
経緯についてはこちらをご参照ください。
■本日の進捗
- Batch Normalizationを理解
■はじめに
今回も「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装(オライリー・ジャパン)」で、深層学習を学んでいきます。
今回はニューラルネットワークの学習を安定に高速に行い、前回学んだ初期化に対してもロバストな手法であるBatch Normalizationを学んでいきます。
■Batch Normalization
Batch Normalizationとはバッチ正規化とも呼ばれ、その名の通り各ミニバッチ内の特徴量を正規化することで、アクティベーションにより各層の入力分布が学習に伴って発生する不安定性の要因となる変化(内部共変量シフト)を低減してくれます。
ミニバッチ内のデータ数をmとすると、各特徴量Bの平均μBと分散σB2は下記で与えられます。
$$ B = \{x_1, x_2, \cdot \cdot \cdot , x_m\} $$
$$ \mu_B = \frac{1}{m} \sum_{i=1}^m x_i $$
$$ \sigma_B^2 = \frac{1}{m} \sum_{i=1}^m ( x_i – \mu_B )^2 $$
各データポイントxiを正規化します。
$$ \hat{x_i} = \frac{x_i – \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} $$
正規化したデータポイントに対して、固有のスケールγとシフトβで変換を行います。
$$ y_i = \gamma \hat{x_i} + \beta $$
正規化で止めると制約が強すぎて(分布が均一になってしまい)、学習が上手くいかない可能性があるため、正規化後のデータ範囲を調整するためのスケールと、出力を移動させて表現を最適にするためのシフトを導入しています。
Batch Normalizationは全結合層(または畳み込み層)などの活性化関数の前(もしくは後)に挿入されます。
■Batch Normalizationの逆伝播
前述の順伝播の出力に対して勾配を求めて行きます。
スケールとシフトの勾配は下記の通りです。
$$ \frac{\partial L}{\partial \gamma} = \sum_{i=1}^m \frac{\partial L}{\partial y_i} \hat{x_i}$$
$$ \frac{\partial L}{\partial \beta} = \sum_{i=1}^m \frac{\partial L}{\partial y_i} $$
次に損失Lの正規化した入力に対する勾配は、
$$ \frac{\partial L}{\partial \hat{x_i}} = \frac{\partial L}{\partial y_i} \cdot \gamma $$
分散σ2と平均μに対する勾配はそれぞれ、
$$ \frac{\partial L}{\partial \sigma^2} = \sum_{i=1}^m \frac{\partial L}{\partial \hat{x_i}} \cdot (x_i – \mu) \cdot \left(- \frac{1}{2} \right) \cdot (\sigma^2 + \epsilon)^{-\frac{3}{2}} $$
$$ \frac{\partial L}{\partial \mu} = \sum_{i=1}^m \frac{\partial L}{\partial \hat{x_i}} \cdot \left( -\frac{1}{\sqrt{\sigma^2} + \epsilon} \right) + \frac{\partial L}{\partial \sigma^2} \cdot \left( -\frac{2}{m} \right) \sum_{i=1}^m (x_i – \mu) $$
ここで、正規化した入力と分散σ2と平均μの入力xに対する勾配が、
$$ \frac{\partial \hat{x_i}}{\partial x_i} = \frac{1}{\sqrt{\sigma^2 + \epsilon }} $$
$$ \frac{\partial \sigma^2}{\partial x_i} = \frac{2(x_i – \mu)}{m} $$
$$ \frac{\partial \mu}{\partial x_i} = \frac{1}{m} $$
以上から、積の微分法則と連鎖律を用いて損失Lに対する入力xの勾配は、
$$ \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial x_i} + \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \sigma^2} \cdot \frac{\partial \sigma^2}{\partial x_i} + \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \mu} \cdot \frac{\partial \mu}{\partial x_i} $$
$$ \ \ \ \ \ \ \ \ \ = \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon }} + \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \sigma^2} \cdot \frac{2(x_i – \mu)}{m} + \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \mu} \cdot \frac{1}{m} $$
よって、
$$ \frac{\partial L}{\partial {x_i}} = \frac{\partial L}{\partial \hat{x_i}} \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \frac{\partial L}{\partial \sigma^2} \cdot \frac{2(x_i – \mu)}{m} + \frac{\partial L}{\partial \mu} \cdot \frac{1}{m} $$
Batch Normalizationの逆伝播は少々複雑に見えますが、偏微分自体にはそれほど難しいところはないので順を追ってひとつずつ勾配を求めて行けば問題ないかと思います。
■Batch Normalizationの実装
上記で示した順伝播と逆伝播の式を基にBatch Normalizationを実装していきます。
class BatchNormalization:
def __init__(self, num_features, epsilon=1e-5, momentum=0.9):
self.epsilon = epsilon
self.momentum = momentum
self.num_features = num_features
self.gamma = np.ones(num_features)
self.beta = np.zeros(num_features)
self.running_mean = np.zeros(num_features)
self.running_var = np.ones(num_features)
self.batch_mean = None
self.batch_var = None
self.x_normalized = None
self.x_centered = None
def forward(self, x, training=True):
if training:
self.batch_mean = np.mean(x, axis=0)
self.batch_var = np.var(x, axis=0)
self.x_centered = x - self.batch_mean
self.x_normalized = self.x_centered / np.sqrt(self.batch_var + self.epsilon)
out = self.gamma * self.x_normalized + self.beta
self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * self.batch_mean
self.running_var = self.momentum * self.running_var + (1 - self.momentum) * self.batch_var
else:
x_normalized = (x - self.running_mean) / np.sqrt(self.running_var + self.epsilon)
out = self.gamma * x_normalized + self.beta
return out
def backward(self, dout):
m = dout.shape[0]
dgamma = np.sum(dout * self.x_normalized, axis=0)
dbeta = np.sum(dout, axis=0)
dx_normalized = dout * self.gamma
dvar = np.sum(dx_normalized * self.x_centered * -0.5 * (self.batch_var + self.epsilon)**-1.5, axis=0)
dmean = np.sum(dx_normalized * -1 / np.sqrt(self.batch_var + self.epsilon), axis=0) + dvar * np.sum(-2 * self.x_centered, axis=0) / m
dx = dx_normalized / np.sqrt(self.batch_var + self.epsilon) + dvar * 2 * self.x_centered / m + dmean / m
return dx, dgamma, dbeta
このBatch Normalizationクラスをニューラルネットワークに実装していきます。今回は、全結合層とReLU層の間に挿入する形で実装します。
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist
class ReLU:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = np.maximum(0, x)
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = np.dot(dout, self.W.T)
return dx
class BatchNormalization:
def __init__(self, num_features, epsilon=1e-5, momentum=0.9):
self.epsilon = epsilon
self.momentum = momentum
self.num_features = num_features
self.gamma = np.ones(num_features)
self.beta = np.zeros(num_features)
self.running_mean = np.zeros(num_features)
self.running_var = np.ones(num_features)
self.batch_mean = None
self.batch_var = None
self.x_normalized = None
self.x_centered = None
def forward(self, x, training=True):
if training:
self.batch_mean = np.mean(x, axis=0)
self.batch_var = np.var(x, axis=0)
self.x_centered = x - self.batch_mean
self.x_normalized = self.x_centered / np.sqrt(self.batch_var + self.epsilon)
out = self.gamma * self.x_normalized + self.beta
self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * self.batch_mean
self.running_var = self.momentum * self.running_var + (1 - self.momentum) * self.batch_var
else:
x_normalized = (x - self.running_mean) / np.sqrt(self.running_var + self.epsilon)
out = self.gamma * x_normalized + self.beta
return out
def backward(self, dout):
m = dout.shape[0]
dgamma = np.sum(dout * self.x_normalized, axis=0)
dbeta = np.sum(dout, axis=0)
dx_normalized = dout * self.gamma
dvar = np.sum(dx_normalized * self.x_centered * -0.5 * (self.batch_var + self.epsilon)**-1.5, axis=0)
dmean = np.sum(dx_normalized * -1 / np.sqrt(self.batch_var + self.epsilon), axis=0) + dvar * np.sum(-2 * self.x_centered, axis=0) / m
dx = dx_normalized / np.sqrt(self.batch_var + self.epsilon) + dvar * 2 * self.x_centered / m + dmean / m
return dx, dgamma, dbeta
class SoftmaxCrossEntropy:
def __init__(self):
self.output = None
self.grad_input = None
def forward(self, logits):
exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
return self.output
def backward(self, y_true):
self.grad_input = self.output - y_true
return self.grad_input
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta)) / y.shape[0]
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
BatchNormalization(hidden_size),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
BatchNormalization(hidden_size),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x, training=True):
for layer in self.layers:
if isinstance(layer, BatchNormalization):
x = layer.forward(x, training)
else:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
if isinstance(layer, BatchNormalization):
dout, _, _ = layer.backward(dout)
else:
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)
lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
loss_history = []
for i in range(step_num):
batch_mask = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_mask]
y_batch = y_train[batch_mask]
loss = network.compute_loss(X_batch, y_batch)
loss_history.append(loss)
network.backward(y_batch)
network.update(lr)
print(f"Step {i+1}, Loss: {loss}")
plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
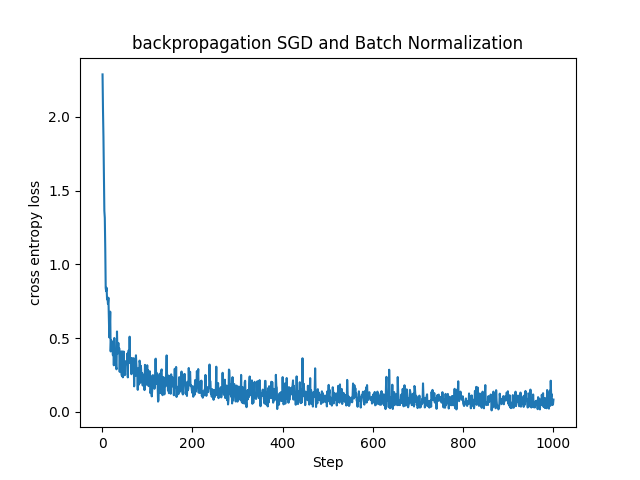
plt.title("backpropagation SGD and Batch Normalization")
plt.show()
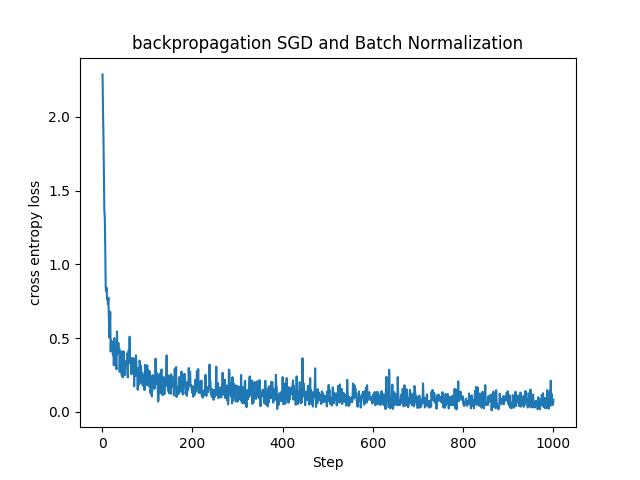
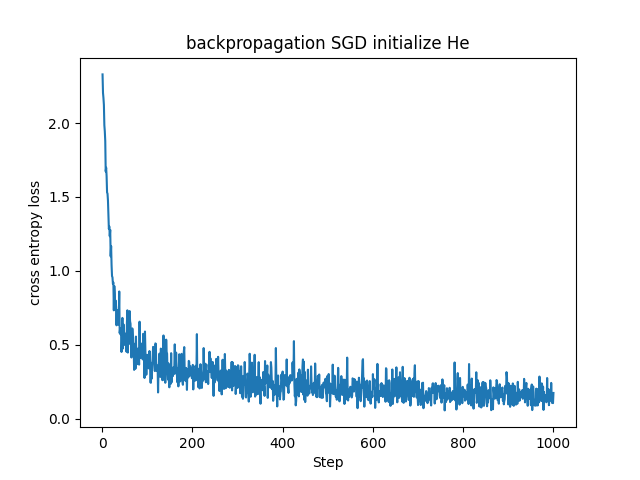
これまで見てきたMNISTデータセットに対する基本的なSGDに比べると損失関数の値が早く小さい値に収束していることが分かります。(参考までに下記に同じパラメータで学習させたSGDとの比較を載せておきます。)
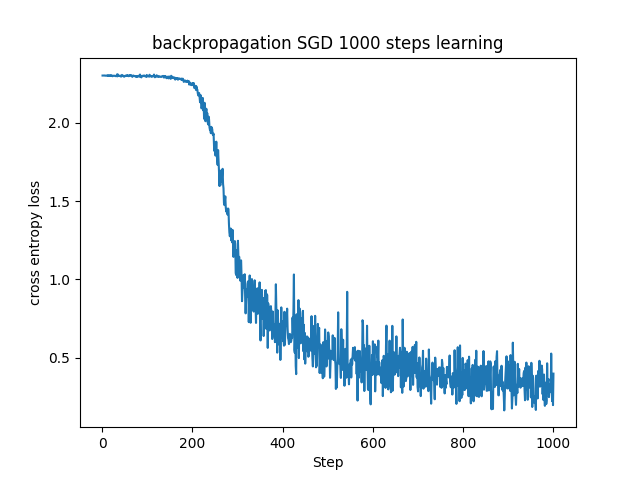
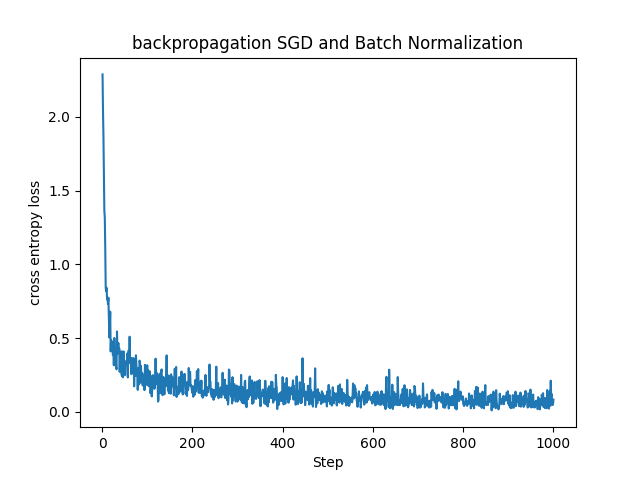
これはHe初期化を用いた場合よりも良い結果でした。
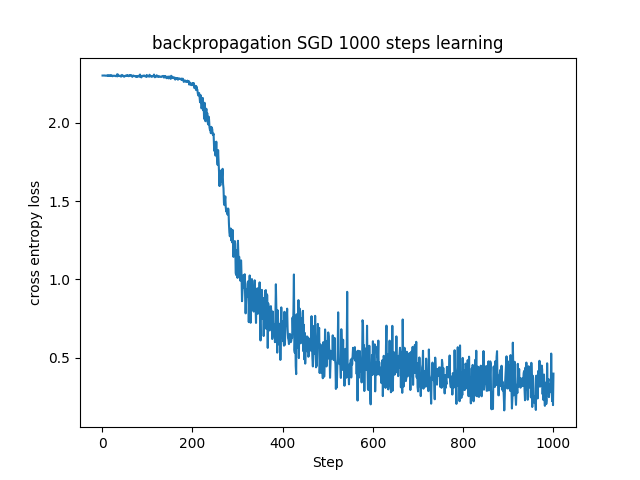
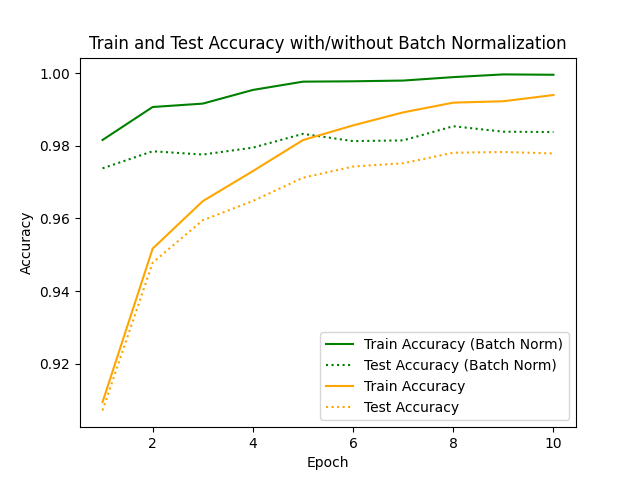
実際にBatch Normalizationを用いた方が早く精度良く学習ができていることが確認できました。
■おわりに
今回は2015年に提唱された比較的新しくも実際に良く用いられているBatch Normalizationを試してみました。正規化するにしては少々込み入ったアルゴリズムでしたが、ただ単に正規化するのではなくスケールとシフトを用いて上手く学習できる手法になっていてなかなか面白いです。
若干コードが長くなりましたが、学習が早いことが確認できているので、処理の重さは問題にならないのでしょう。これまでのところで言えば入れておいて悪いことはないのではないでしょうか。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html
- PyTorch documentation. pytorch.org. https://pytorch.org/docs/stable/index.html
- Batch Normalization: Accelerating Deep NetWork Training by Reducing Internal Covariate Shift. Sergey Ioffe, Christian Szegedy. 2015. Google Inc.