活性化関数

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day51

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

Sigmoid関数を理解
ReLU関数を理解

■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

前回、単純パーセプトロンでは表現できない線形分離不可能な問題を多層パーセプトロンに拡張することで表現できるようになることを学びました。今回はこれをニューラルネットワークに拡張するために非線形活性化関数を学んでいきます。

■活性化関数

活性化関数（activation function）とは、ニューロンに与える入力の総和がどのように活性化（発火）するかを決定するための関数です。

これまでに出てきたヘヴィサイド階段関数（あるいは単位階段関数）も活性化関数のひとつです。

$$ \begin{eqnarray} H(x) = \begin{cases} 0 & (x \lt 0 ) \\ 1 & (x \gt 0 ) \end{cases} \end{eqnarray} $$

パーセプトロンはこのような階段関数を活性化関数として用います。（というより本当の意味では階段関数を活性化関数に用いるニューラルネットワークがパーセプトロンというべきでしょうか。）つまり、多層パーセプトロンは既にニューラルネットワークの一種ですが、一般的なニューラルネットワークと区別するのは、主にこの活性化関数に何を用いるかの違いになります。

活性化関数は階段関数のような非線形関数であることが求められます。線形関数ではいけない理由は、線形関数では多層を持たせたり、ニューロンを繋いでいく意味がないからです。

$$ h(x) = cx$$

$$ y(x) = h(h(h(w_1 x_1 + w_2 x_2+ b))) = c^3(w_1 x_1 + w_2 x_2 + b) $$

$$ h(x) = c^3x \ \ \ \ とすれば単純パーセプトロンと等価 $$

■シグモイド関数

シグモイド関数（sigmoid function）は、かつて最も広く用いられた活性化関数で、下記のように定義されます。

$$ \sigma (x) = \frac{1}{1+e^{-x}} $$

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.title("Sigmoid Function")
plt.ylabel("y")
plt.xlabel("x")
plt.show()

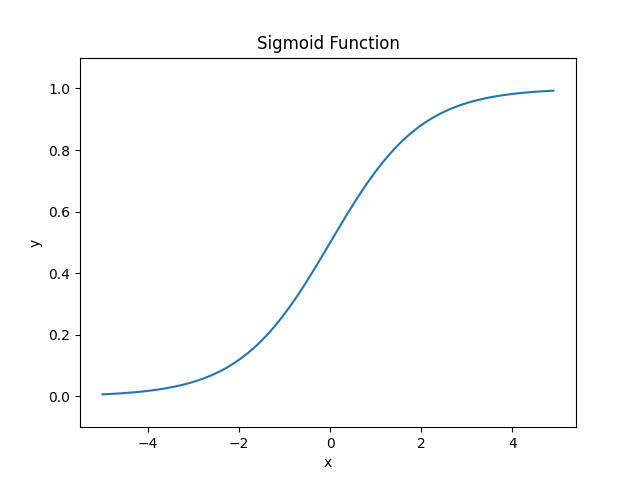
シグモイド関数は入力値を0から1の間に圧縮する連続値を返し、微分可能です。しかし、変曲点から離れたy=0やy=1に収束する範囲での勾配がなくなっていくこと（勾配消失）や、常に正の値を取りゼロ中心でないことが深層学習において問題になることがあります。

ニューラルネットワーク全体をシグモイド関数を用いて記述してみます。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def identity_function(x):
    return x

def a(x, W, b):
    a = np.dot(x, W) + b
    return a

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = a(x, W1, b1)
    z1 = sigmoid(a1)
    a2 = a(z1, W2, b2)
    z2 =sigmoid(a2)
    a3 = a(z2, W3, b3)
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network,x)
print("y = {}".format(y))

y = [0.31682708 0.69627909]

■ReLU

ReLU（rectified linear unit）は、一般的にランプ関数と呼ばれる正規化線形関数で、入力値が0以下なら0を返し、入力値が0を超えていれば値をそのまま返す関数です。

$$ \begin{eqnarray} h(x) = \begin{cases} x & (x \gt 0 ) \\ 0 & (x \le 0 ) \end{cases} \end{eqnarray} $$

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.xlim(-5.5, 5.5)
plt.title("ReLU")
plt.ylabel("y")
plt.xlabel("x")
plt.show()

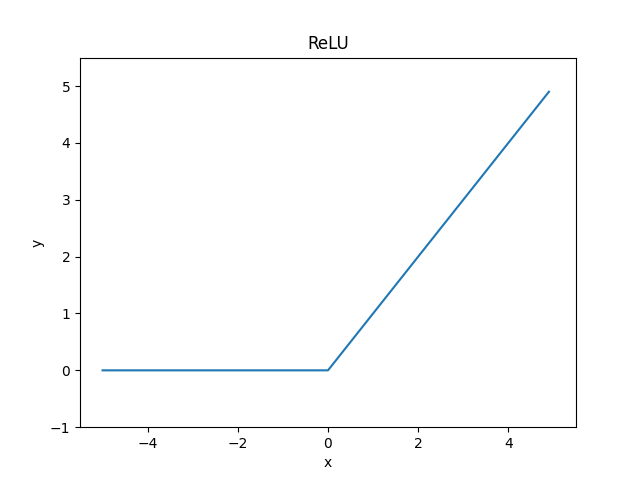
ReLUは非常にシンプルなため計算コストが少なく、入力値が正である時のみ勾配を持つため、このスパース性が学習を効率的にすると言われています。シグモイド関数で言及された勾配消失も起こりづらいですが、負の入力が多いと勾配が0になってしまい、意味を持たなくなってしまいます。また、勾配が大きくなりすぎるという問題も含んでいます。

同様にニューラルネットワークの活性化関数としてReLUを導入してみます。

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

def identity_function(x):
    return x

def a(x, W, b):
    a = np.dot(x, W) + b
    return a

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # a1 = np.dot(x, W1) + b1
    a1 = a(x, W1, b1)
    z1 = relu(a1)
    # a2 = np.dot(z1, W2) + b2
    a2 = a(z1, W2, b2)
    z2 =relu(a2)
    # a3 = np.dot(z2, W3) + b3
    a3 = a(z2, W3, b3)
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network,x)
print("y = {}".format(y))

y = [0.426 0.912]

■おわりに

今回は多層パーセプトロンに対して活性化関数としてシグモイド関数やReLUを導入することで簡単なニューラルネットワークを構築することができました。

■参考文献

Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田秀基訳. オライリー・ジャパン. 2017. 392p.
斎藤康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html