AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day49
経緯についてはこちらをご参照ください。
■本日の進捗
- 単純パーセプトロンを理解
■はじめに
100日間継続すると決めた当初、どうしようもないくらい機械学習に関する知見はゼロでしたが、良書と巡り合うことができたおかげで約半分の50日弱で機械学習について一通り広く浅く知ることができ、自分でデータセットを探してきて、データフレームなどを用いて中身を見て、新たなモジュールを追加することで基本的な機械学習モデルを作ることまではできるようになりました。(もちろんその理論や背景も広く浅く理解したつもりではあります。)
ただ当初の想定より自分の学習ペースは良くなくて、社畜の余暇でももう少しやれたかと思わないこともないので、残りの半分はもう少し深い(文字通り深い)ところに入っていきたいと思います。
未だに機械学習を用いて何をするかは決めていないですが、やっぱり新しいことに触れるのは楽しいので、よりAIっぽい(バカっぽい?)深層学習に触れていきたいと思います。
2冊目として選んだのは「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装(オライリー・ジャパン)」で、これを教師としてもう少しただの勉強を続けていきます。
本書の前半は既に知っている内容なので読み飛ばして、まずは深層学習の元祖と言われる単純パーセプトロンからです。
■単純パーセプトロン
単純パーセプトロン(simple perceptron)とは、生物の神経網を模した人工ニューラルネットワークの最も基本的なアルゴリズムで、1950年代にフランク・ローゼンブラット(Frank Rosenblatt)によって開発された歴史のある2クラス分類アルゴリズムです。
生物の神経網がニューロン同士をシナプスを介して繋がるように、パーセプトロンも入力から出力までの各ニューロン(ノード)が重みを介して繋がっています。
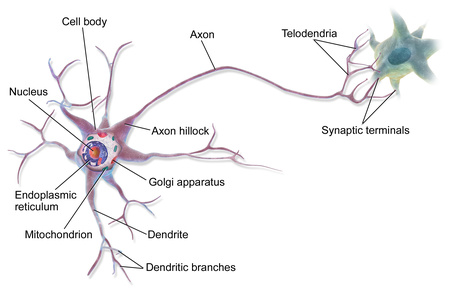
(ニューラルネットワーク Wikipediaより)
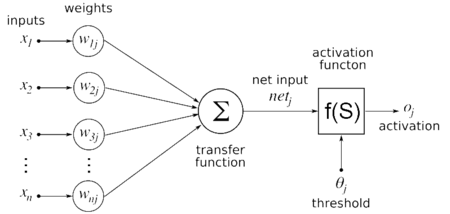
(ニューラルネットワーク Wikipediaより)
入力が2つだけの場合を考えればとても単純で、下記のように記述できます。
$$ \begin{eqnarray} y = \begin{cases} 0 & (w_1 x_1 + w_2 w_2 \leq \theta ) \\ 1 & (w_1 x_1 + w_2 x_2 \gt \theta ) \end{cases} \end{eqnarray} $$
入力に対して重みが乗っかり、その総和が閾値θを超えるとニューロンが発火して出力を与えます。
このモデルに1次関数と同様にバイアス(切片と同じ役割で線形をシフトさせることができる)を導入すると下記のようにも記述できます。
$$ \begin{eqnarray} y = \begin{cases} 0 & (b + w_1 x_1 + w_2 w_2 \leq \theta ) \\ 1 & (b + w_1 x_1 + w_2 x_2 \gt \theta ) \end{cases} \end{eqnarray} $$
ここまで一緒に学んできた方は、おっ!っと思うかもしれませんが、線形モデルに非常によく似ています。
■形式ニューロン
実は単純パーセプトロンは形式ニューロンと呼ばれる論理ゲートを参考に開発されました。
$$ \begin{eqnarray} H(x) = \begin{cases} 0 & (x \lt 0 ) \\ 1 & (x \gt 0 ) \end{cases} \end{eqnarray} $$
各論理ゲートはヘヴィサイド階段関数 H(Heaviside step function)を上のように定義し、0か1の入力値を取る場合、下記のように記述できます。
●ANDゲート
ANDゲートは入力がどちらも1(x1=1 AND x2=1)の時に出力が1になります。
$$ y = H( w_1 x_1 + w_2 x_2 + b) \ \ \ ただし、w_1=1, \ w_2=1, \ b=-1.5 $$
●NANDゲート
NANDゲートはANDゲートの反対で、入力がどちらも1の時、出力が0になります。(Not AND)
$$ y = H( w_1 x_1 + w_2 x_2 + b) \ \ \ ただし、w_1=-1, \ w_2=-1, \ b=1.5 $$
●ORゲート
ORゲートは入力のどちらかが1(x1=1 OR x2=1)の時、出力が1になります。
$$ y = H( w_1 x_1 + w_2 x_2 + b) \ \ \ ただし、w_1=1, \ w_2=1, \ b=-0.5 $$
■パーセプトロンを書いてみる
前述の形式ニューロンをパーセプトロンで書いてみます。(関数がヘヴィサイド階段関数から単位階段関数にになっているので注意)
import numpy as np
def SimplePerceptron(x1, x2, w1, w2, b):
x = np.array([x1, x2])
w = np.array([w1, w2])
result = np.sum(w*x) + b
return result
def StepFunction(x):
if x <= 0:
return 0
else:
return 1
def AND(x1_and, x2_and):
result_and = SimplePerceptron(x1_and, x2_and, 1, 1, -1.5)
y_and = StepFunction(result_and)
return y_and
def NAND(x1_nand, x2_nand):
result_nand = SimplePerceptron(x1_nand, x2_nand, -1, -1, 1.5)
y_nand = StepFunction(result_nand)
return y_nand
def OR(x1_or, x2_or):
result_or = SimplePerceptron(x1_or, x2_or, 1, 1, -0.5)
y_or = StepFunction(result_or)
return y_or
print("When x1 = 1, x2 = 1")
print("AND: y={}".format(AND(1, 1)))
print("NAND: y={}".format(NAND(1, 1)))
print("OR: y={}".format(OR(1, 1)))
print("")
print("When x1 = 1, x2 = 0")
print("AND: y={}".format(AND(1, 0)))
print("NAND: y={}".format(NAND(1, 0)))
print("OR: y={}".format(OR(1, 0)))
When x1 = 1, x2 = 1
AND: y=1
NAND: y=0
OR: y=1
When x1 = 1, x2 = 0
AND: y=0
NAND: y=1
OR: y=1形式ニューロンの項目で紹介した各論理ゲートの挙動通りの結果になっています。
これは単純パーセプトロンを用いれば今回挙げた論理ゲートは再現できるということに他なりません。論理ゲートはコンピュータに用いられる2進数を表現するためにも使われ、よくコンピュータが0と1から成ると表現されるように、今回のパーセプトロンも0か1を入力値として0か1を返すアルゴリズムでした。
つまりパーセプトロンでコンピュータを作ることも説明することもできるということです。
■おわりに
今回はディープラーニングの前身である単純パーセプトロンで論理ゲートを再現するコードを書いてみました。実はここからが面白いのですが、自分の体力が限界を迎えてきたので今日はこの辺にしようかと思います。
次回、単純パーセプトロンの限界。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html