AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day35
経緯についてはこちらをご参照ください。
■本日の進捗
●適合率、再現率、f-値、支持率を理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
今回は単にモデルの予測精度(R2スコアやAccuracy)を追い求めるのではなく、本来の目的に沿った評価基準を学んでいきます。
■2クラス分類における評価基準
これまで学習モデルの予測精度をなるべく汎化性能を保った形で評価するために、交差検証やネスト(nested cross-validation)を導入してデータによるバイアスや過剰適合がないようにその精度を追い求めてきました。
では、ここまであらゆる事象に考慮した手法を用いて学習させたモデルは僕らの目的を完全に満たしたものなのでしょうか?
機械学習モデルを構築する本来の目的に立ち戻って考えてみると、本当に欲しいモデルというのは、その道の熟練者があなたの横についていなくてもそれと同等のレベルで結果を予測することができるようになることではないでしょうか。経験豊富な医師がいなくても画像データから病気の初期診断ができる医療スクリーニング、ホワイトハッカーがいなくてもマルウェアを検知することができるアンチウイルスソフト、認知能力の高いドライバーでなくても人や障害物にぶつからない自動運転システムなどです。
例えば医療スクリーニングを例にとれば、入力データを見て陽性(どちらでも良いのだが医療系では一般には病気であること)か陰性かを判断します。これまでの評価基準で言えばAccuracyなので、陰性を陽性と分類(偽陽性:タイプⅠエラー)しても、陽性を陰性と分類(偽陰性:タイプⅡエラー)しても、その割合が低ければ優秀なモデルでした。つまり多少病気を見逃しても全体の正答率が高ければ優秀ということです。その”多少”の患者としてはたまったものではありません。このアプリケーションに関しては、偽陽性は許容(患者に余計な検査や心労をかけることにはなるが)できても、偽陰性が一切ないことが最も良いモデルということになります。
■混同行列
混同行列(confusion matrix)とは、クラス分類モデルの性能を評価するための手法で、下記の要素で構成されます。
真陽性(True Positive, TP)
モデルが陽性を正しく分類したサンプル
偽陽性(False Positive, FP)
モデルが陰性を誤って陽性と分類したサンプル(タイプⅠエラー)
偽陰性(False Negative, FN)
モデルが陽性を誤って陰性と分類したサンプル(タイプⅡエラー)
真陰性(True Negative, TN)
モデルが陰性を正しく分類したサンプル
Predicted
| Positive | Negative |
-------------------------------
Actual | TP | FN | Positive
-------------------------------
| FP | TN | Negativeまずは医療スクリーニングを想定して30特徴量を持つNegative(Class0)とPositive(Class1)の2クラス分類データセットを作ってみます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
n_samples = 500
n_features = 30
X, y = make_classification(n_samples=n_samples, n_features=n_features,
n_informative=5, n_redundant=10, n_repeated=5,
n_clusters_per_class=1, class_sep=2, flip_y=0.1,
random_state=8)
feature_names = [f"Feature{i}" for i in range(1, n_features+1)]
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
fig, axes = plt.subplots(nrows=6, ncols=5, figsize=(20, 15))
axes = axes.flatten()
for i, feature in enumerate(feature_names):
axes[i].hist(df[df['target'] == 0][feature], bins=15, color='green', alpha=0.6, label='Class 0')
axes[i].hist(df[df['target'] == 1][feature], bins=15, color='orange', alpha=0.6, label='Class 1')
axes[i].set_title(feature)
axes[i].legend()
plt.tight_layout()
plt.show()
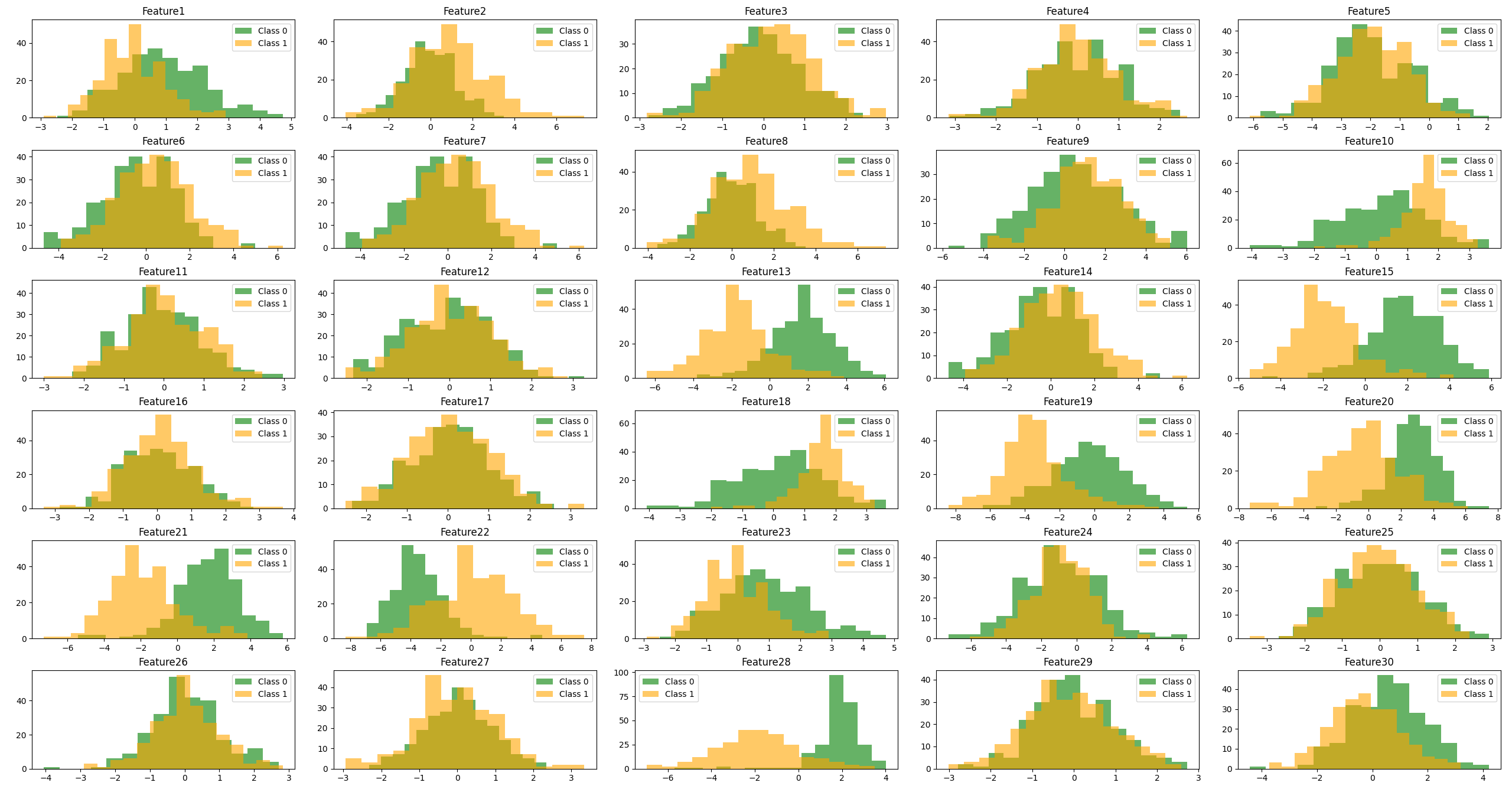
有意な特徴量は5つでそのどれもがわずかにラップしているので予測が難しそうです。精度の高い決定木で学習させてその混合行列を表示してみます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay
n_samples = 500
n_features = 30
X, y = make_classification(n_samples=n_samples, n_features=n_features,
n_informative=5, n_redundant=10, n_repeated=5,
n_clusters_per_class=1, class_sep=2, flip_y=0.1,
random_state=8)
feature_names = [f"Feature{i}" for i in range(1, n_features+1)]
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
model = DecisionTreeClassifier(random_state=8)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy: {:.2f}'.format(accuracy))
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=model.classes_)
disp.plot(cmap='Blues')
plt.title('Confusion Matrix')
plt.show()
Accuracy: 0.93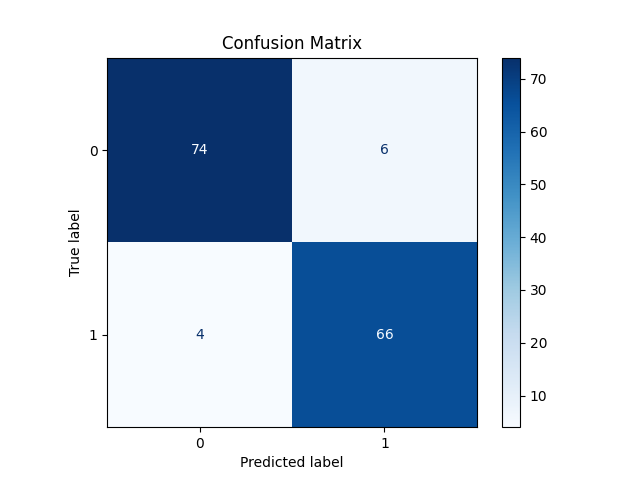
スコアは0.93ととても良いですが、偽陽性が4つあるのに対して偽陰性が6つもあります。Accuracyは下記の式で算出されています。
$$ \mathrm{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} $$
■適合率と再現率
混同行列を指標化する方法はAccuracy以外にもあり、最もよく使われるのが適合率と再現率です。
適合率(precision)は、モデルが陽性と予測したうち、実際に陽性だった割合を示します。つまりどれだけ正しく陽性を識別できたかということです。これは適合率(陽性的中率、positive predictive value:PPV)とも言われます。
$$ \mathrm{Precision} = \frac{TP}{TP + FP} $$
先ほどの混同行列で言えばPrecision=0.95となります。
再現率(recall)は、実際に陽性であるサンプルの中で、モデルが正しく陽性と予測できた割合を示します。つまり実際の陽性をどれだけ見逃さなかったかということになります。これは感度(sensitivity)、ヒット率(hit rate)、真陽性率(true positive rate:TRP)とも言われます。
$$ \mathrm{Recall} = \frac{TP}{TP + FN} $$
先ほどの混同行列で言えばRecall=0.93となります。
■f-値
適合率と再現率は先ほどのような医療スクリーニング用(自作の擬きデータですが)データセットの場合は再現率の方が遥かに重要ということになります。
ではこの再現率を上げるためにはどうしたらいいでしょうか?
再現率はすべての陽性の中で正しく陽性と予測できる数が増えればそのスコアは上がっていくことになります。ならば入力データをすべて陽性と返すアルゴリズム()を作ってみたら再現率は必ず1になるのではないでしょうか。
このような目的から逸脱した精度向上にならないよう、適合率と再現率をさらにまとめたf-値(f1スコア)という指標があります。
$$ \mathrm{f1} = 2 \times \frac{\mathrm{Precision} \times \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}} $$
f-値は適合率と再現率のトレードオフ関係を考慮する際ににはとても有用ですが、直観的ではなく解釈が難しい指標でもあります。
■classification_reprt
最後にこれらの指標を簡単に出力できるclassification_reportクラスを使ってその数値を確認してみたいと思います。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay, classification_report
n_samples = 500
n_features = 30
X, y = make_classification(n_samples=n_samples, n_features=n_features,
n_informative=5, n_redundant=10, n_repeated=5,
n_clusters_per_class=1, class_sep=2, flip_y=0.1,
random_state=8)
feature_names = [f"Feature{i}" for i in range(1, n_features+1)]
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
model = DecisionTreeClassifier(random_state=8)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
report = classification_report(y_test, y_pred, target_names=['Class 0', 'Class 1'])
print(report)
precision recall f1-score support
Class 0 0.95 0.93 0.94 80
Class 1 0.92 0.94 0.93 70
accuracy 0.93 150
macro avg 0.93 0.93 0.93 150
weighted avg 0.93 0.93 0.93 150ここで支持率(support)とは、クラス分類における各クラスの実際のサンプル数を意味します。例えば元のデータセットにClass0のサンプルが80個ある場合、Class0の支持率は80となります。
再現率を上げるために、正規化してからロジスティック回帰で学習しなおしてみます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay, classification_report
n_samples = 500
n_features = 30
X, y = make_classification(n_samples=n_samples, n_features=n_features,
n_informative=5, n_redundant=10, n_repeated=5,
n_clusters_per_class=1, class_sep=2, flip_y=0.1,
random_state=8)
feature_names = [f"Feature{i}" for i in range(1, n_features+1)]
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
model = LogisticRegression(random_state=8)
model.fit(X_train_scaled, y_train)
y_pred = model.predict(X_test_scaled)
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy: {:.2f}'.format(accuracy))
report = classification_report(y_test, y_pred, target_names=['Class 0', 'Class 1'])
print(report)
Accuracy: 0.98
precision recall f1-score support
Class 0 0.99 0.97 0.98 80
Class 1 0.97 0.99 0.98 70
accuracy 0.98 150
macro avg 0.98 0.98 0.98 150
weighted avg 0.98 0.98 0.98 150■おわりに
ここまで様々なモデル構築手法や評価指標を学んできましたが、すべてにおいて重要なのは本来の目的に沿った選択をしていくということではないでしょうか。何事においても万能なものというのはないので、常に最終的な目的を見失わないことが重要ですね。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html