AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day26
経緯についてはこちらをご参照ください。
■本日の進捗
●多項式特徴量を理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
前回の交互作用特徴量に続いて多項式特徴量を学んでいきます。
■多項式特徴量
多項式特徴量(polynomial Features)とは、これまで見てきたビニングや交互作用特徴量と同様に新たな特徴量を生成する手法です。考え方は良く知られたもので、既にある特徴量の多項式を加えるだけです。
こちらも線形モデルが非線形な振る舞いを学習できるようにするのですが、高次の多項式を加えることでモデルが複雑化し、汎化性能が下がる過剰適合のリスクが高まります。
交互作用特徴量との大きな違いは、任意に高次の項を生成できることです。特徴量同士の積である相互作用項のみを追加する交互作用特徴量とは次元数が大きく異なる可能性があり、これが精度向上にも計算コスト増大にも繋がるため適切な次数の選択が必要になります。
まずは交互作用特徴量の記事で学習させたモデルを振り返ります。
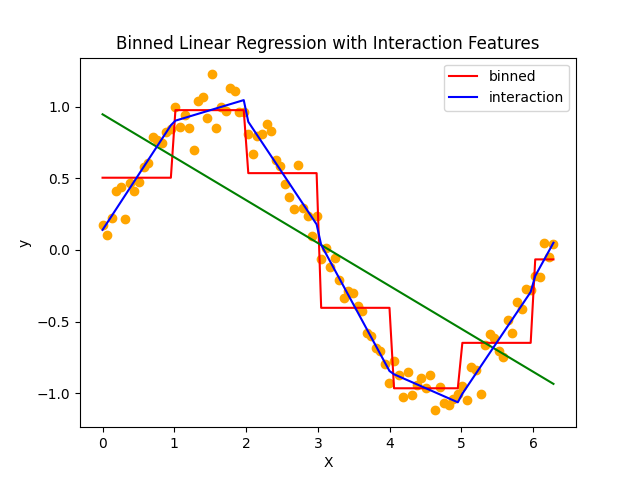
改めて眺めてみると、わずかに線(青線が交互作用特徴量を追加したsin波の予測モデル)がガタついてるものの線形回帰アルゴリズムを一切いじっていないにしては実態のデータプロットに上手く沿っています。
このデータセットに対して多項式特徴量を加えた場合、上記モデルからどのように変化するのかを見てみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import OneHotEncoder, PolynomialFeatures
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
bins = np.linspace(0, 6, 11)
which_bin = np.digitize(X, bins=bins)
encoder = OneHotEncoder(sparse_output=False)
X_binned = encoder.fit_transform(which_bin)
model_binned = LinearRegression()
model_binned.fit(X_binned, y)
y_binned_pred = model_binned.predict(X_binned)
plt.plot(X, y_binned_pred, color='red', label='binned')
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X, y)
X_poly = poly.fit_transform(X)
model_poly = LinearRegression()
model_poly.fit(X_poly, y)
y_poly_pred = model_poly.predict(X_poly)
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
plt.scatter(X, y, color='orange')
plt.plot(X, y_pred, color='green')
plt.plot(X, y_poly_pred, color='blue', label='polynomial')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Polynomial Linear Regression')
plt.show()
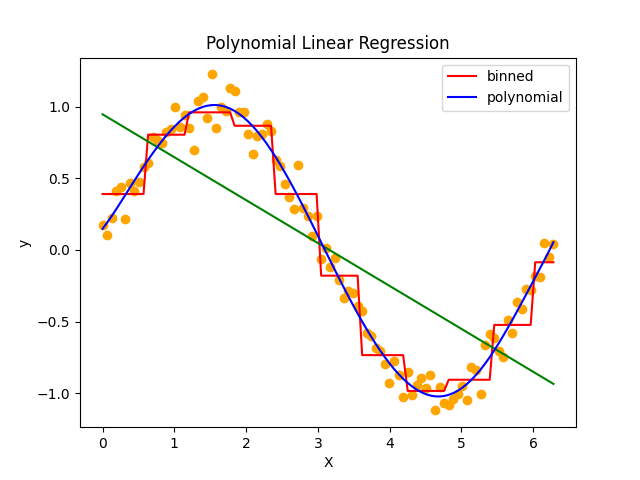
良く見慣れた多項式回帰の線になってきました。多項式特徴量を用いればビニングすらせずに滑らかなモデルを学習させることができました。
今回は10次の多項式を用いて学習させてみましたが、数学的な背景がある方には3次で十分なことが理解できるでしょう。(このデータセットはとても軽いので10次でも重くはないのですが。)しかし、非常に高次の多項式を導入すると、過剰適合やルンゲ現象による振動が起こります。
折角なのでいくつか試してみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
np.random.seed(0)
X = np.linspace(0, 2 * np.pi, 100).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.1, size=X.shape)
degrees = [2, 3, 10, 20, 40, 60, 80, 100]
plt.figure(figsize=(12, 18))
for i, degree in enumerate(degrees, 1):
poly = PolynomialFeatures(degree=degree, include_bias=False)
X_poly = poly.fit_transform(X)
model_poly = LinearRegression()
model_poly.fit(X_poly, y)
y_poly_pred = model_poly.predict(X_poly)
plt.subplot(4, 2, i)
plt.scatter(X, y, color='orange', label='Original Data', alpha=0.5)
plt.plot(X, y_poly_pred, color='blue', label=f'Polynomial Degree {degree}')
plt.title(f'Polynomial Regression (Degree={degree})')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.tight_layout()
plt.show()
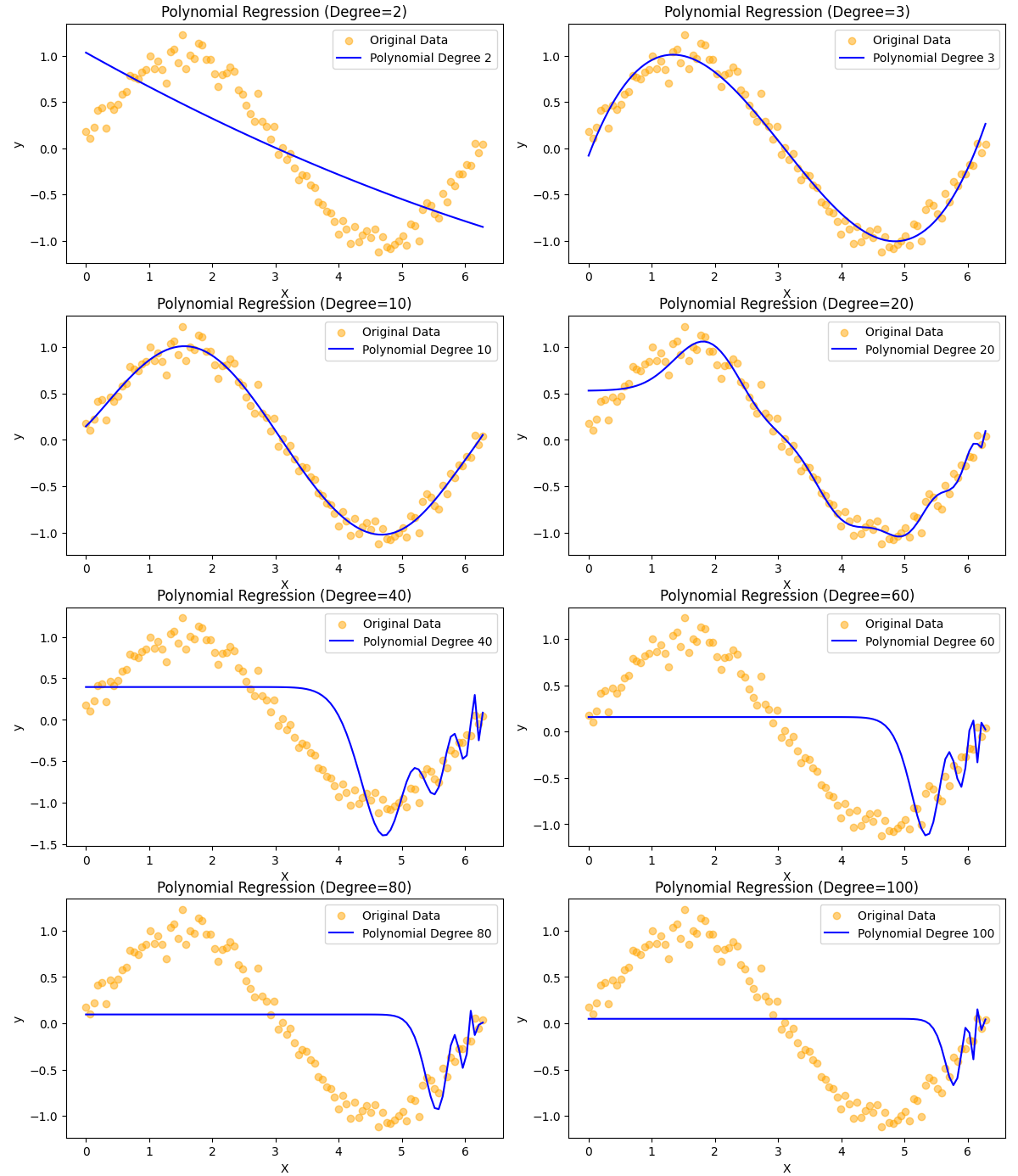
あれだけ精度の良かった多項式特徴量を加えた線形回帰モデルが、degree=20あたりでは振動し始めて予測を外してしまってます。ちなみにこれ以上の次数にするとオバーフローの可能性が高いので試しませんが、精度が良くなることはないと容易に想像が付きます。
■おわりに
通常の数学のようにスプライン曲線による近似手法などは、PolynomialFeaturesクラスの範囲を超えるので、多項式特徴量でモデル精度向上を図るには適切な次数を特定し、引数として渡してあげる必要がありそうです。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html