AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day18
経緯についてはこちらをご参照ください。
■本日の進捗
●NMFを理解
■はじめに
引き続き「Pythonではじめる機械学習(オライリー・ジャパン)」で学んでいきます。
前回のPCA同様に、前処理で次元削減としても使える教師なし学習手法であるNMFを取り上げます。
■NMF
非負値行列因子分解(NMF:Non-negative Matrix Factorization)とは、1つの行列(V)を2つの行列(W, H)に分解するもので、特徴量の抽出や次元削減を行うことができます。
目的関数は下記の通りで、W≥0, H≥0ということが求められます。(ここから非負値行列と言います。)
$$ L(W, H) = 0.5 * || X – WH ||^2_{loss} $$
非負成分を非負係数で重み付き和を取ることで、必ず加法的な構成要素を返すため、お互いに打ち消しあうことがなく(PCA等に比べて)データを理解しやすい形で分解してくれるという特徴があります。
例えば顔の画像データセットに対してNMFを用いると、顔のパーツごと(目や鼻や口など)に自動的に分解してくれることもあり、主成分という形よりも理解しやすい傾向にあります。ただし局所最適解しか見つけられない傾向も持ち合わせています。(これは非負制約によるものです)
また、乱数初期化を行うため、結果に乱数性があることも注意したいところです。
参考までに前回も用いたLabeled Faces In Wildデータセットにk-NNで学習させたクラス分類の結果を再掲しておきます。
Test Accuracy: 19.37%同じデータセットに対してNMFを適用して、次元数を最適化してみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.decomposition import NMF
lfw_people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
X = lfw_people.data
y = lfw_people.target
n_samples, h, w = lfw_people.images.shape
unique, counts = np.unique(y, return_counts=True)
max_images_per_person = 50
limited_indices = []
for i in range(len(unique)):
indices = np.where(y == unique[i])[0]
limited_indices.extend(indices[:max_images_per_person])
limited_indices = np.array(limited_indices)
X_people = X[limited_indices]
y_people = y[limited_indices]
X_scaled = X_people / 255.0
components_range = list(range(10, 201, 10))
scores = []
for n_components in components_range:
nmf = NMF(n_components=n_components, max_iter=4000, random_state=8, solver='mu')
X_nmf = nmf.fit_transform(X_scaled)
X_train, X_test, y_train, y_test = train_test_split(X_nmf, y_people, test_size=0.2, random_state=8)
knn = KNeighborsClassifier(n_neighbors=1, n_jobs=-1)
knn.fit(X_train, y_train)
score = knn.score(X_test, y_test)
scores.append(score)
print(f'n_components = {n_components}, Accuracy = {score * 100:.2f}%')
plt.figure(figsize=(10, 6))
plt.plot(components_range, scores, marker='o')
plt.title('k-NN Accuracy with Different NMF Components')
plt.xlabel('Number of NMF Components')
plt.ylabel('Accuracy')
plt.grid(True)
plt.show()
n_components = 10, Accuracy = 12.59%
n_components = 20, Accuracy = 17.68%
n_components = 30, Accuracy = 19.37%
n_components = 40, Accuracy = 27.12%
n_components = 50, Accuracy = 25.67%
n_components = 60, Accuracy = 27.36%
n_components = 70, Accuracy = 26.88%
n_components = 80, Accuracy = 32.20%
n_components = 90, Accuracy = 28.09%
n_components = 100, Accuracy = 29.30%
n_components = 110, Accuracy = 32.45%
n_components = 120, Accuracy = 31.48%
n_components = 130, Accuracy = 30.27%
n_components = 140, Accuracy = 28.09%
n_components = 150, Accuracy = 30.51%
n_components = 160, Accuracy = 30.27%
n_components = 170, Accuracy = 28.81%
n_components = 180, Accuracy = 28.81%
n_components = 190, Accuracy = 29.06%
n_components = 200, Accuracy = 28.57%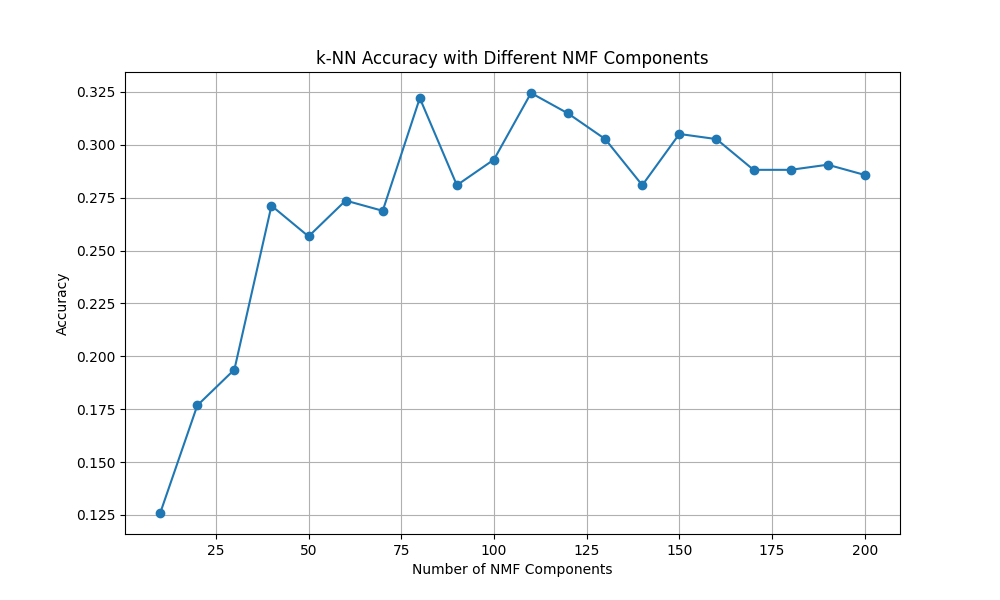
次元数110あたりが一番良さそうで、PCAより僅かにk-NNの性能が上がっています。
ちなみに収束性があまり良くなくmax_iterを4000まで上げていますが、シングルコアではかなり時間がかかるので、solverをmu(乗法更新法、デフォルトは座標降下法:cd)を採用し、k-NNも並列化(AMD 12core 4.40GHz)しています。おかげさまで学習は一瞬で終わります。
この設定の中で最適化した110次元の中身を見てみたいので、NMFが抽出した規定行列を特徴量として可視化してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import NMF
lfw_people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
X = lfw_people.data
n_samples, h, w = lfw_people.images.shape
X_scaled = X / 255.0
n_components = 110
nmf = NMF(n_components=n_components, max_iter=4000, random_state=8, solver='mu')
W = nmf.fit_transform(X_scaled)
H = nmf.components_
plt.figure(figsize=(10, 10))
for i in range(min(16, n_components)):
plt.subplot(4, 4, i + 1)
component_image = H[i].reshape(h, w) + 0.5
component_image = np.clip(component_image, 0, 1)
plt.imshow(component_image, cmap='gray')
plt.title(f'Component {i + 1}')
plt.axis('off')
plt.tight_layout()
plt.show()

これらがNMFが分離した特徴量になります。顔全体がはっきりしているものは多くなく、右半分だったり頭(おでこ?)などの部分ごとで分離している様子も確認できます。その他表情だったり光の当たり方、襟といった特定の部位など様々な観点から画像の特徴を捉えていることが分かります。
また、NMFの基底行列の順番に意味がないこともよく理解できます。今回は最初の16個を表示してみましたが、明らかに110次元の中で上位16位以内に重要そうとは思えないような画像も含んでいます。各コンポーネントは完全に独立して特徴を捉えているので、多種多様な特徴が並んでいるわけです。
■おわりに
今回のNMFも前処理としてある一定の結果を出しましたが、NMF単体でも教師なし学習として人の顔画像から特徴を抽出できることを学びました。
また、今回初めてscikit-learnで並列化処理をしてみました。クラスによってできないものもあるのですが、これだけイタレーション数が増えてくるとやっぱり並列化は大事ですね。こんなに簡単に並列処理できてしまうことも、大人気ライブラリの大きなメリットではないでしょうか。
ちなみに単体でGPU化はできないみたいですが、他のライブラリを噛ませることで可能なようです。GPUはF1を4画面(+iPad F1 App.)で見たいがために存在している個人PCとしてはそこそこのもの(RTX4070Ti Super)を積んでいるので是非試してみたいところです。
実は他のPython処理で「-gpu」オプションをやった時は新しい世界が見えました。NVIDIAが世界一の会社になるわけですね。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html