AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day14
経緯についてはこちらをご参照ください。
前回の内容は下記をご参照ください。
■本日の進捗
●カーネル法サポートベクターマシンの理解
■はじめに
線形モデルについて学んだ記事にも登場した線形サポートベクターマシンに対して、より複雑なモデルに適用可能なカーネル法を用いたサポートベクターマシンというものがあります。今回はこの拡張版SVMをクラス分類問題に適用していきたいと思います。
■2つのサポートベクターマシン
●線形サポートベクターマシン
線形に分離できるような(比較的シンプルで)明確な違いのあるデータセットに対して有効で、その名の通りデータ空間をマージンを持った直線、または平面で分類します。マージンと誤分類の調整パラメータを持つため、モデルの学習曲線を容易に調節できることを学びました。
●カーネル法を用いたサポートベクターマシン
線形に分離できないような非線形データを含むデータセットにも有効で、特徴表現にデータを写像し、その特徴空間内で線形に分離できるように学習します。ただ、データポイントの拡張を、どのデータでどのくらいすればいいのかは分からないことも多いので、闇雲にデータポイントを拡張していては計算コストの際限ない増加を招いてしまう可能性があります。
特徴表現におけるデータポイント間の距離を拡張を計算せずに直接学習させる数学的なトリックがあります。これはカーネルトリックと呼ばれ、サポートベクターマシンにおいては、多項式カーネル(polynomial kernel)とガウシアンカーネル(radial basis function : RBF)がよく用いられています。
■データの次元拡張
まずはカーネルトリックを使わずに、データポイントを拡張する効果を見ていきたいと思います。
今回はscikit-learn標準のmake circlesデータセットで、ランダムな非線形データを作成してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
plt.legend(handles=scatter.legend_elements()[0], labels=['Class 0', 'Class 1'], title='Classes')
plt.title('Non-linear Dataset')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.show()
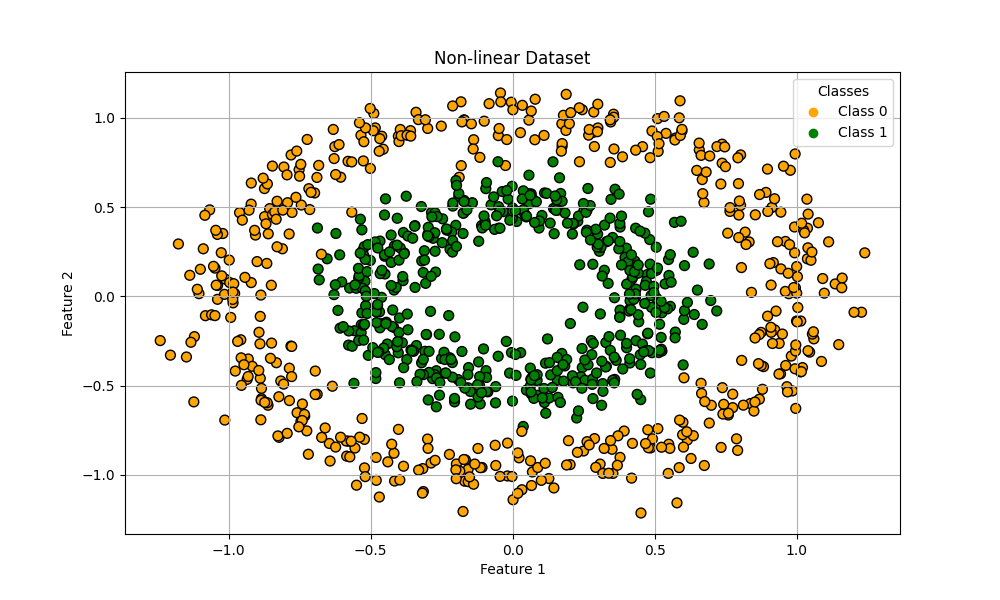
うわあ…明らかに直線で分類できそうもない酷いデータセットが出来上がりました笑
ちょっと可哀そうな気もしますが、線形サポートベクターマシンでクラス分類してみます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
model = LinearSVC()
model.fit(X_train, y_train)
print("train score: {}".format(model.score(X_train, y_train)))
print("test score: {}".format(model.score(X_test, y_test)))
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), levels=np.arange(-0.5, 2, 1))
plt.contour(xx, yy, Z, alpha=0.8, levels=[0], linewidths=2, colors='black')
plt.scatter([], [], c='green', label='Class 1')
plt.scatter([], [], c='orange', label='Class 0')
plt.legend(title='Classes')
plt.title('Linear SVM')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.show()
train score: 0.5714285714285714
test score: 0.5633333333333334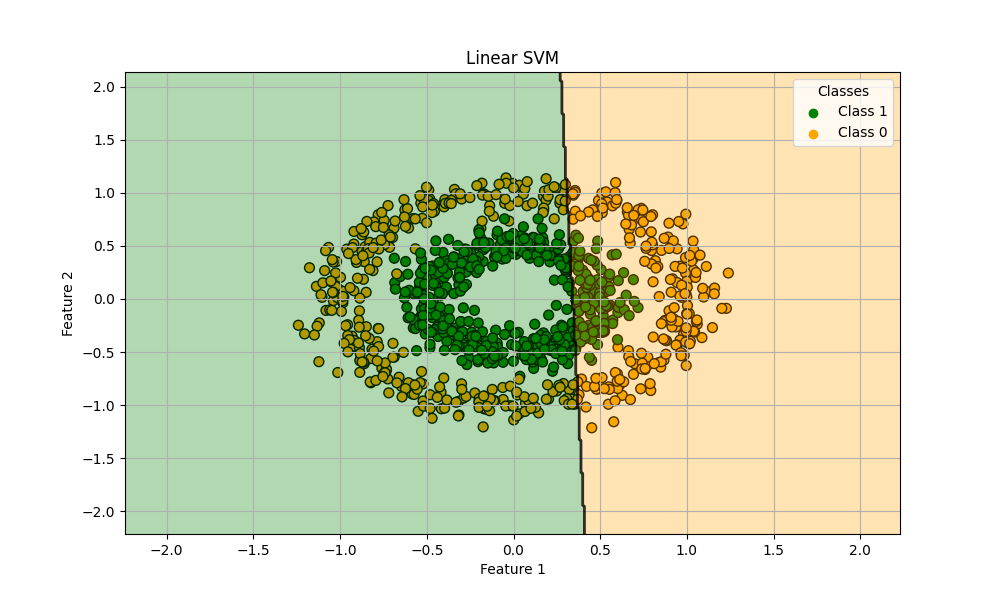
よく頑張りました。混乱しながら学習してくれている様子が思い浮かびます。人にもアルゴリズムにも向き不向きというものがあります。線形サポートベクターマシンが悪いわけではないことを心に留めておいてください。
Feature1に対して2乗をしたものを3次元目のデータとして加えて3Dプロットしてみました。
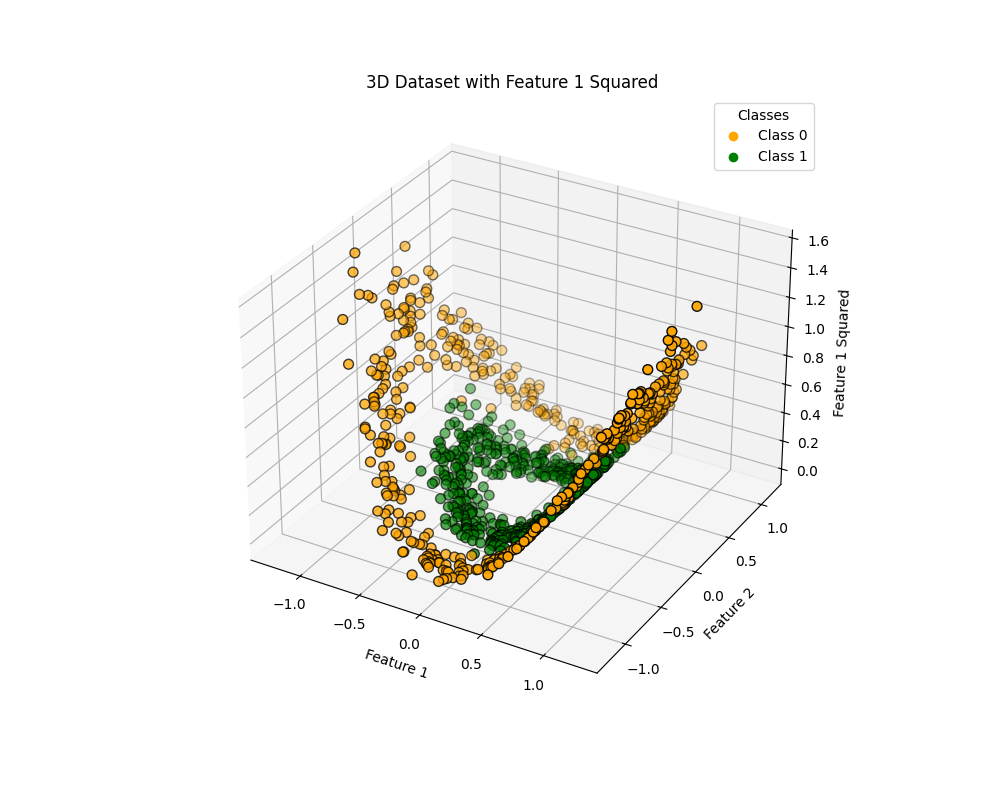
3次元目の軸を拡張できたので、先ほどと同様に線形サポートベクターマシンで学習させてみます。果たして変化はあるのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
Z = X[:, 0] ** 2
X_squared = np.column_stack((X[:, 0], X[:, 1], Z))
X_train, X_test, y_train, y_test = train_test_split(X_squared, y, test_size=0.3, random_state=8)
model = LinearSVC()
model.fit(X_train, y_train)
print("train score: {}".format(model.score(X_train, y_train)))
print("test score: {}".format(model.score(X_test, y_test)))
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(X_squared[:, 0], X_squared[:, 1], Z, c=y, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
x_min, x_max = X_squared[:, 0].min() - 1, X_squared[:, 0].max() + 1
y_min, y_max = X_squared[:, 1].min() - 1, X_squared[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z_decision = model.decision_function(np.c_[xx.ravel(), yy.ravel(), (xx.ravel() ** 2)])
Z_decision = Z_decision.reshape(xx.shape)
ax.plot_surface(xx, yy, Z_decision, alpha=0.5, color='black', linewidth=0, antialiased=True)
ax.set_title('Linear SVM')
ax.set_xlabel('Feature 1')
ax.set_ylabel('Feature 2')
ax.set_zlabel('Feature 1 Squared')
plt.show()
train score: 0.7871428571428571
test score: 0.7666666666666667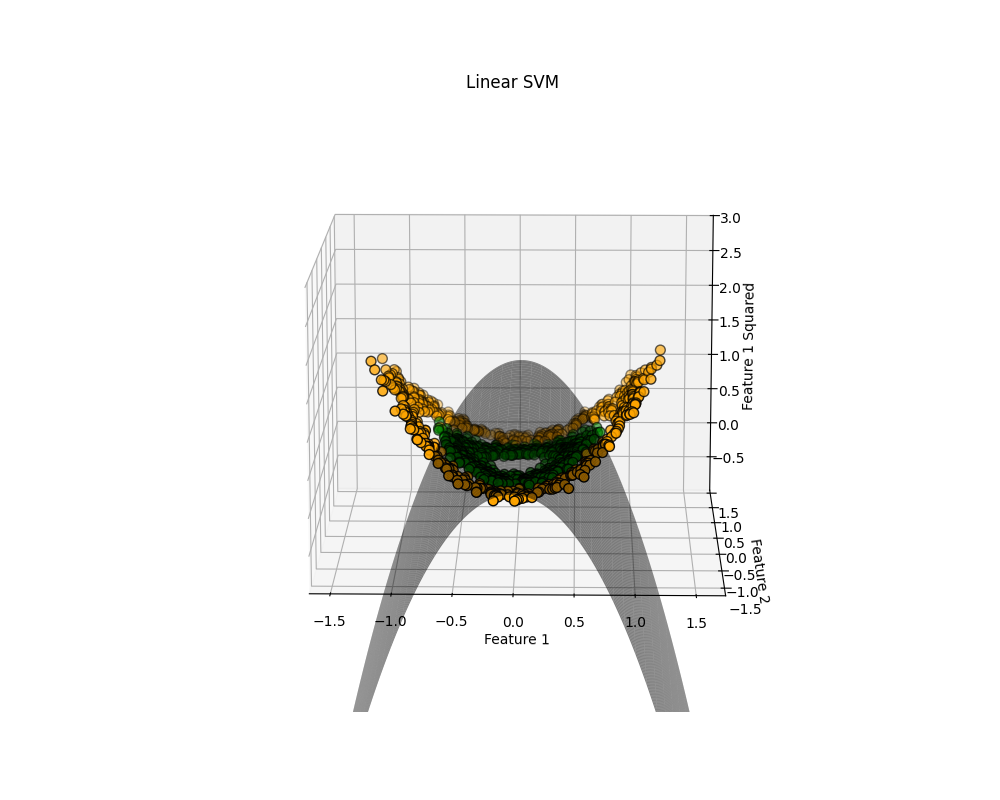
可視化が難しいのですが、決定境界がどうなっているかは何となく分かると思います。このように単に元のデータを拡張しただけでスコアは大幅に改善しました。線形モデルのポテンシャルの高さを感じます。
■カーネルトリック
サポートベクターマシンは決定境界の決定(頭痛が痛い)にデータポイントの重要度を学習しています。このデータポイントは決定境界に位置する一部を抽出していて、これらのデータポイントをサポートベクターといいます。
この距離(データポイントとサポートベクターの距離)の測定にはガウシアンカーネルを用います。
$$ k_{rbf} (x_1, x_2) = \exp (-\gamma || x_1 \ – \ x_2 ||^2) $$
xはデータポイントで、γはガウシアンカーネル幅を制御するパラメータです。
早速先ほどのデータセットにガウシアンカーネル法サポートベクターマシンを適用してみます。単なる次元拡張に比べてどの程度の改善があるのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
model = SVC(kernel='rbf', C=1.0, gamma=0.5)
model.fit(X_train, y_train)
print("train score: {}".format(model.score(X_train, y_train)))
print("test score: {}".format(model.score(X_test, y_test)))
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), levels=np.arange(-0.5, 2, 1))
plt.contour(xx, yy, Z, alpha=0.8, levels=[0], linewidths=2, colors='black')
plt.scatter([], [], c='green', label='Class 1')
plt.scatter([], [], c='orange', label='Class 0')
plt.legend(title='Classes')
plt.title('Gaussian Kernel SVM')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.show()
train score: 0.9928571428571429
test score: 0.9866666666666667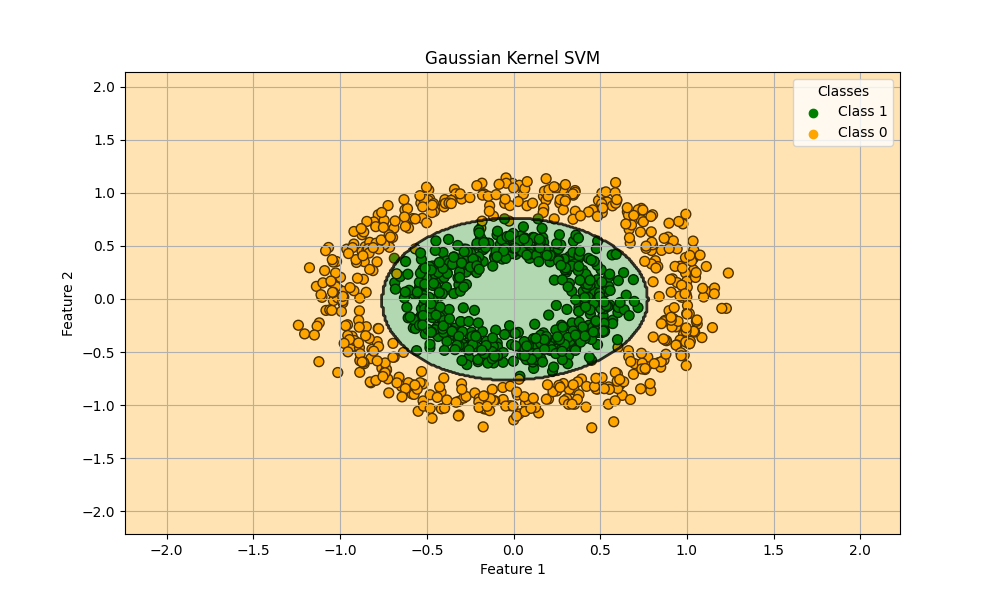
何ということでしょう。ほぼ完璧に分類できています。カーネルトリック恐るべし…
もう既に凄まじい精度ですが、後学のために今回は1.0に設定したC値と0.5に設定したgammaをそれぞれ振ってその挙動を見てみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.5, random_state=8)
C_values = [0.1, 1.0, 1000]
gamma_values = [0.1, 1.0, 10]
fig, axs = plt.subplots(len(C_values), len(gamma_values), figsize=(15, 15))
for i, C in enumerate(C_values):
for j, gamma in enumerate(gamma_values):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
model = SVC(kernel='rbf', C=C, gamma=gamma)
model.fit(X_train, y_train)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax = axs[i, j]
ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), edgecolors='k', s=50)
ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.colors.ListedColormap(['orange', 'green']), levels=np.arange(-0.5, 2, 1))
ax.contour(xx, yy, Z, alpha=0.8, levels=[0], linewidths=2, colors='black')
ax.set_title(f'C={C}, gamma={gamma}')
ax.set_xlabel('Feature 1')
ax.set_ylabel('Feature 2')
ax.grid()
plt.scatter([], [], c='green', label='Class 1')
plt.scatter([], [], c='orange', label='Class 0')
plt.legend(title='Classes', loc='upper right', bbox_to_anchor=(1.2, 1))
plt.tight_layout()
plt.show()
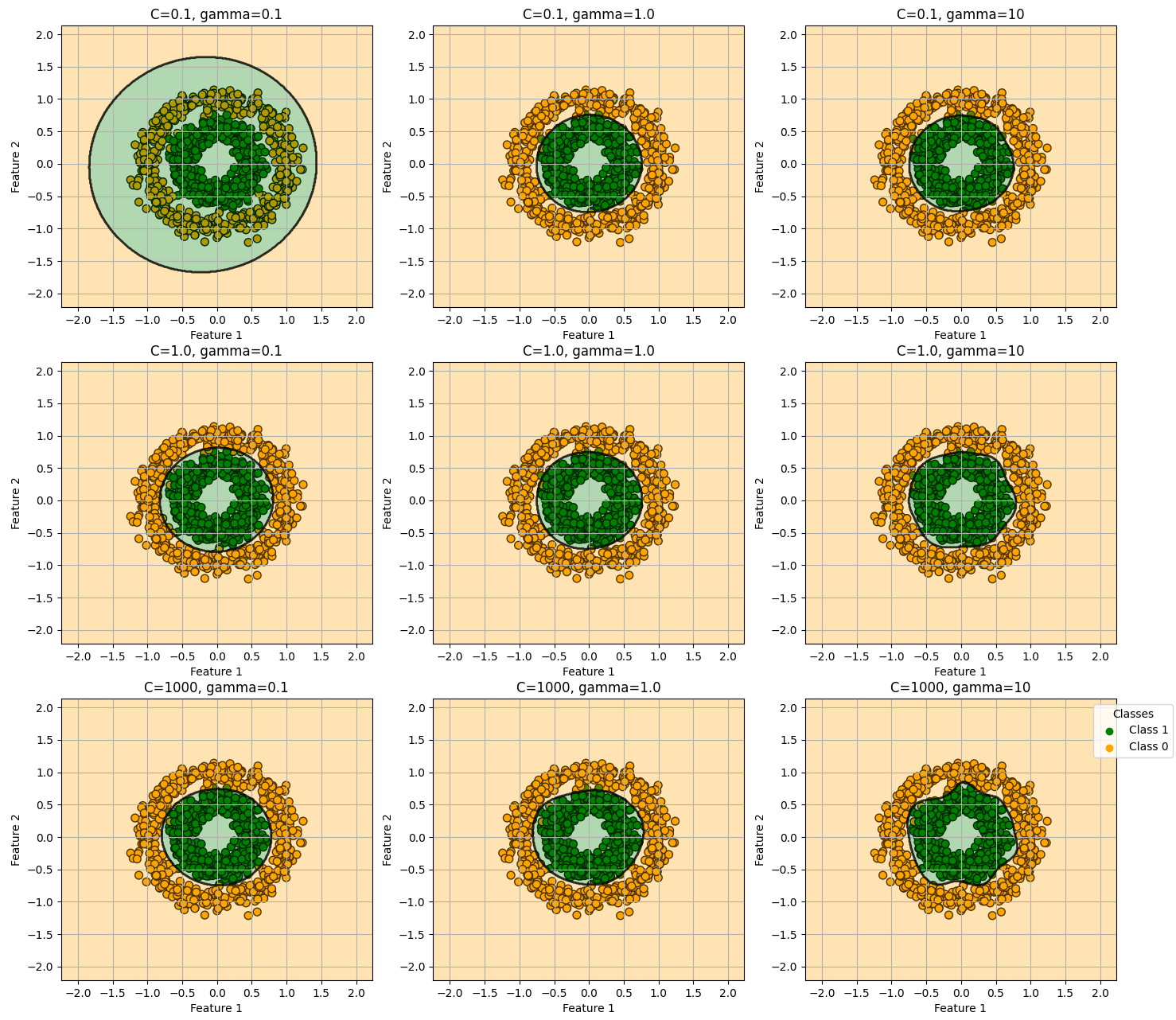
C値とgammaが大きくなるほど(図の右下に行くほど)個々のデータポイントに対して影響を強く受けていることが分かります。このパラメータを弄ることで汎化性能を調整することができそうですね。
■おわりに
今回のタイトルは、いつの日かAIが人生における教訓すらも我々人間に教えてくれるのではないかという希望を込めて付けました。
最初に見たように明らかに線形モデルで学習するべきではないデータに出会った時、普通は線形モデルでは予測は無理だから他のモデルを試そうと思うでしょう。でも実際はどうでしたか?次元を拡張するという何でもない前処理をするだけで実用に十分な精度を出せたことに留まらず、カーネルトリックを用いてさらにその性能を上げることを体験できました。このモデルの背景には線形モデルの可能性に賭けて(正しく人生を賭けて)モデルの改良に取り組んできた研究者達がいたからこそ、今日普通に使われているのかと思います。彼らの努力と信念に感服いたしました。
皆さんも是非とも自分の限界を自分で決めることなく、その先を、そしてその遥か先を目指して日々精進していただければと思います。
だって、線形モデルは自分の限界を超えてみせたんですから。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html