AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day10
経緯についてはこちらをご参照ください。
前回の内容はこちらをご参照ください。
■本日の進捗
●k-最近傍法を使えるようになる
■はじめに
初日から1日も空けることなく遂に10日目です!
ここまでNumPy, pandas, matplotlib, SciPyというPythonライブラリを学び、ようやくscikit-learnを通じて機械学習に入ってきました。「Pythonではじめる機械学習」はもう10日で40ページも進んでしまいました()
今日もk-NNで遊んでいきたいと思います。
■k-NNを様々なデータセットで試してみた (その2)
前回の「k-最近傍法で遊ぶ」では、scikit-learn標準のあやめデータセットとワインデータセットをk-NNに適用し、k値の最適化やデータのスケーリングをしてテストデータに対して良いスコアを出せるモデルを構築していきました。
ただ、これらのあやめデータセットやワインデータセットはどちらも低次元なデータでした。k-NNは高次元データが苦手と言われているので、今回はまずscikit-learn標準の高次元(正確にはこれでもまだまだ高次元ではないのだが…)データセットである数字(digits)データセットで遊んでみたいと思います。
digits datasetを見てみる
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
data = load_digits()
print("data shape: {}".format(data.data.shape))
plt.figure(figsize=(10, 5))
for index in range(10):
plt.subplot(2, 5, index + 1)
plt.imshow(data.images[index], cmap='gray')
plt.title(f'Label: {data.target[index]}')
plt.axis('off')
plt.tight_layout()
plt.show()

data shape: (1797, 64)ぼんやり数字に見えてきましたか?「2」はなかなかにあれですが、お察しの通りこの数字データセットは0から9までの”手書き”の数字画像が集められたものです。さらに64の特徴量があると分かりましたが、これはこの画像が8×8ピクセルで構成されていて、その1ピクセルごとの濃淡が数値化されて格納されていると思っていただければ間違いないと思います。
これらの値がどのように格納されているのか見てみます。
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
data = load_digits()
print("data shape: {}".format(data.data.shape))
plt.figure(figsize=(10, 5))
for index in range(10):
plt.subplot(2, 5, index + 1)
plt.imshow(data.images[index], cmap='gray')
plt.title(f'Label: {data.target[index]}')
plt.axis('off')
plt.tight_layout()
plt.show()
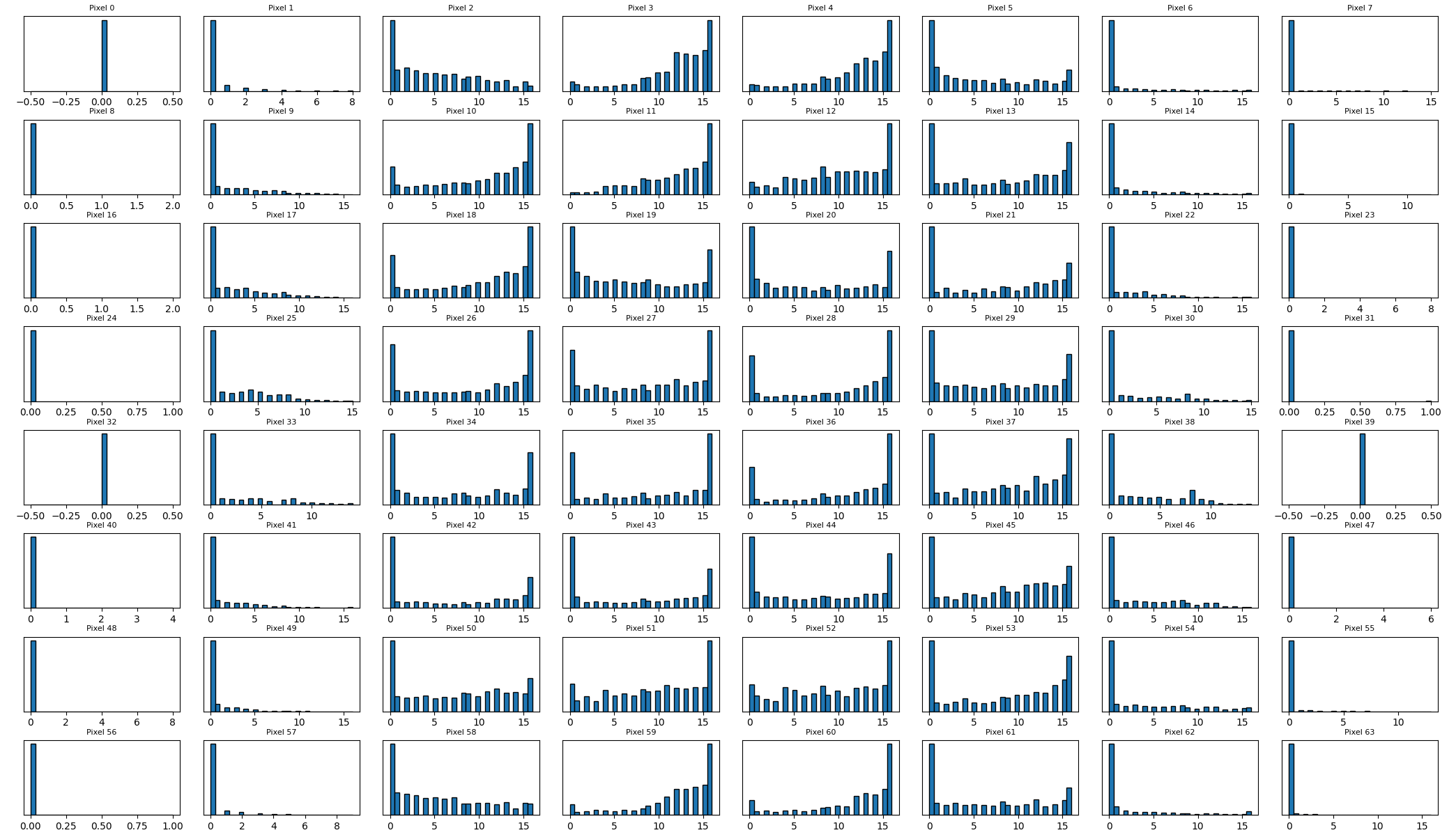
これまでで最も高次元なので見づらいですが、数字が存在する頻度が低い画面の端の方では偏りが大きいものの、ほとんどすべての特徴量でスケールが均一です。
前回見たワインデータセットでは0.2から1600程度まで広範囲にデータが及んでいました。それに比べると今回はスケーリングせずとも良い精度が見込めそうです。このままk-NNに突っ込んでみようと思います。(怠慢なわけではないですよ。事前にデータをちゃんと見ろとミュラー先生に言われただけです。)
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
data = load_digits()
X = data.data
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
train_scores = []
test_scores = []
for k in k_range:
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
train_scores.append(train_score)
test_score = model.score(X_test, y_test)
test_scores.append(test_score)
optimal_k = k_range[np.argmax(test_scores)]
print(f'Optimal k: {optimal_k}')
print(f"Best Test Score: {test_scores[np.argmax(test_scores)]}")
plt.figure(figsize=(12, 6))
plt.plot(k_range, train_scores, marker='o', linestyle='-', color='orange', label='Training Accuracy')
plt.plot(k_range, test_scores, marker='o', linestyle='-', color='g', label='Test Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN: Training and Test Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
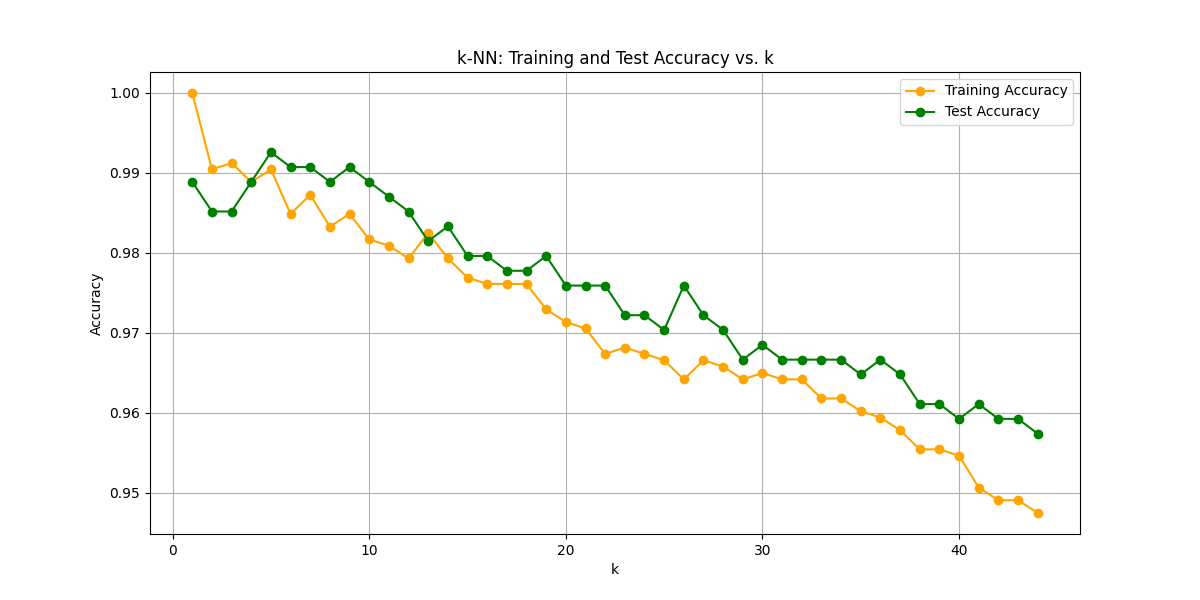
Optimal k: 5
Best Test Score: 0.9925925925925926k=5辺りではトレーニングデータでのスコアをテストデータでのスコアが上回っていて、なおかつkが増えていくとスコアが下がっていきます。k=5は最適なモデルと言って良さそうです。なお、スコアは心配になるほど好成績です笑
このモデルでいいのかは一抹の不安が残りますが、打てる手はあまりないのでクラス分類におけるk-NNはここで締めたいと思います。
■回帰にも適用してみる
最も単純な機械学習アルゴリズム 「怠惰学習」でも言及したように、k-NNはクラス分類(あやめの品種や数字の違いなどの不連続値)だけではなく、回帰(連続値)にも適用できる優秀な機械学習アルゴリズムです。
実は回帰の方が理解がしやすいと思っていて、トレーニングデータが散布図(後記)に表現されている様子を思い浮かべてみてください。新しいデータをその散布図にプロットした時に、周りにあるk個の最も近い値の平均を取る様子を想像してみればクラス分類よりもk-NNの挙動が分かりやすいのではないでしょうか。
サンプルにscikit-learn標準データセットからCalifornia housingデータセットを用いてみます。このデータセットはカリフォルニアの世帯収入、築年数、1住宅当たりの平均部屋数、平均寝室数、人口、1住宅当たりの平均居住者数、緯度、経度の特徴量8つを持っています。ターゲット変数は住宅の中央値価格になります。これを散布図に表示してみます。
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
import pandas as pd
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['Target'] = data.target
plt.figure(figsize=(14, 10))
for i, col in enumerate(data.feature_names):
plt.subplot(3, 3, i + 1)
plt.scatter(df[col], df['Target'], alpha=0.5)
plt.title(f'{col} vs Target')
plt.xlabel(col)
plt.ylabel('Target')
plt.tight_layout()
plt.show()
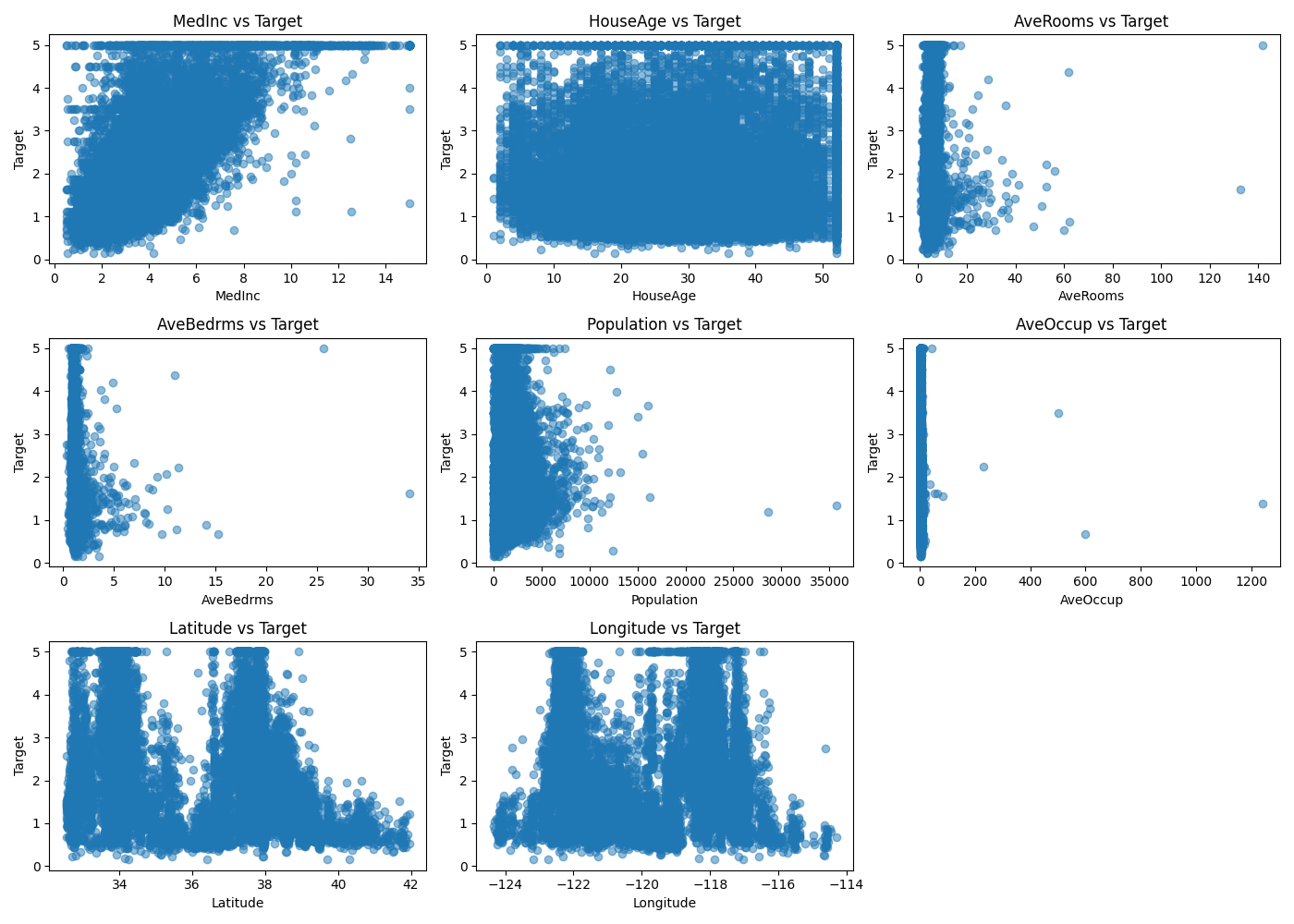
一見するとスケールは不均一に見えますが、k-NNはどの程度正しく判別できるのでしょうか。
実際にk-NN回帰に突っ込んでいきます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
data = fetch_california_housing()
X = data.data
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
train_scores = []
test_scores = []
for k in k_range:
model = KNeighborsRegressor(n_neighbors=k)
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
train_scores.append(train_score)
test_score = model.score(X_test, y_test)
test_scores.append(test_score)
optimal_k = k_range[np.argmax(test_scores)]
print(f'Optimal k: {optimal_k}')
print(f"Best Test Score: {test_scores[np.argmax(test_scores)]}")
plt.figure(figsize=(12, 6))
plt.plot(k_range, train_scores, marker='o', linestyle='-', color='orange', label='Training Accuracy')
plt.plot(k_range, test_scores, marker='o', linestyle='-', color='g', label='Test Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN Regressor: Training and Test Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
Optimal k: 8
Best Test Score: 0.1344508338264162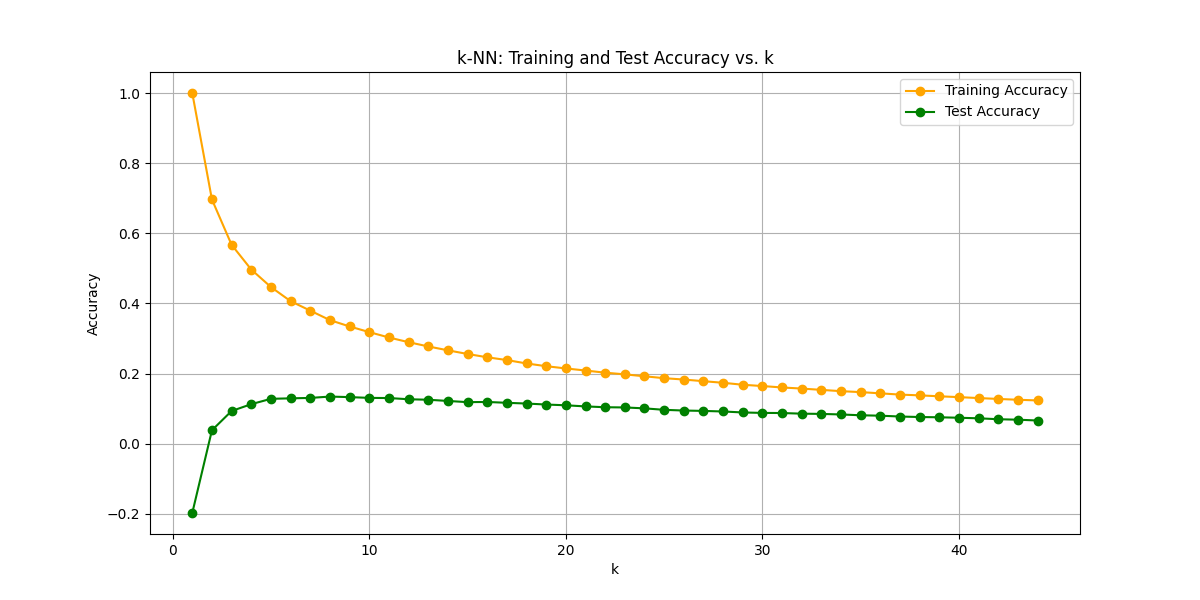
スコアが絶望的に低いです。恐らくスケールが不均一だからでしょう。標準化でスケーリングしてから再度k-NN回帰に突っ込んでみます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import StandardScaler
data = fetch_california_housing()
scaler = StandardScaler()
df = pd.DataFrame(data.data, columns=data.feature_names)
scaled_data = scaler.fit_transform(df)
df_scaled = pd.DataFrame(scaled_data, columns=data.feature_names)
X = df_scaled
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=8)
k_range = range(1, 45)
train_scores = []
test_scores = []
for k in k_range:
model = KNeighborsRegressor(n_neighbors=k)
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)
train_scores.append(train_score)
test_score = model.score(X_test, y_test)
test_scores.append(test_score)
optimal_k = k_range[np.argmax(test_scores)]
print(f'Optimal k: {optimal_k}')
print(f"Best Test Score: {test_scores[np.argmax(test_scores)]}")
plt.figure(figsize=(12, 6))
plt.plot(k_range, train_scores, marker='o', linestyle='-', color='orange', label='Training Accuracy')
plt.plot(k_range, test_scores, marker='o', linestyle='-', color='g', label='Test Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('k-NN Regressor Scaled: Training and Test Accuracy vs. k')
plt.legend()
plt.grid(True)
plt.show()
Optimal k: 9
Best Test Score: 0.6846035916300747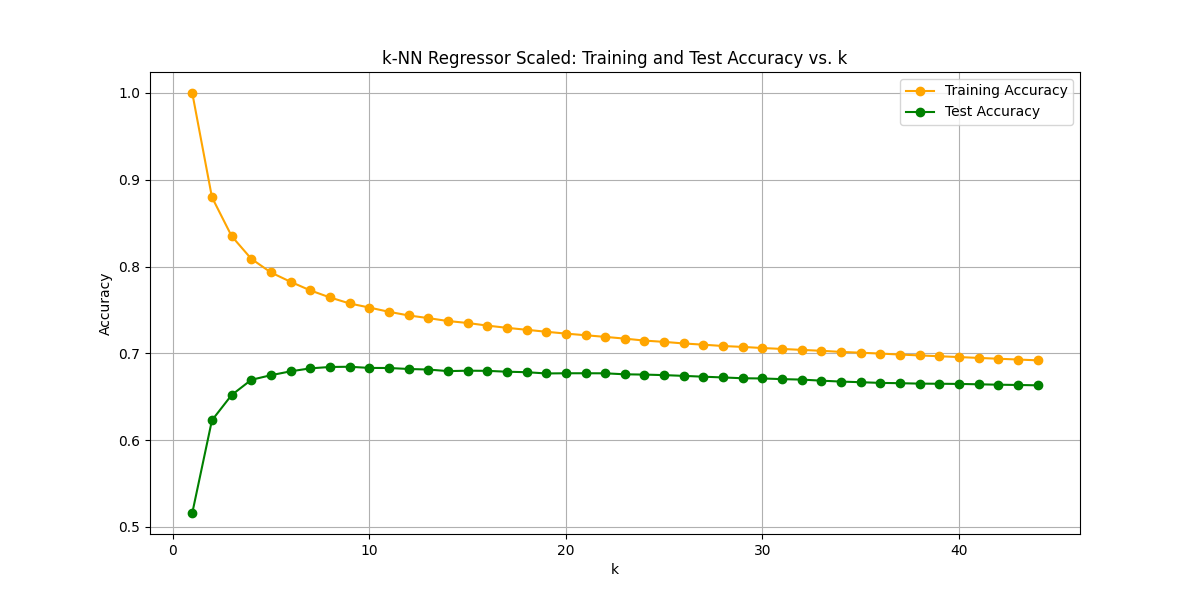
予想通り大幅に改善しました。(学習曲線がなめらかなのは整った綺麗なデータだからだと思われます。)トレーニングデータでのスコアを超えることはできなかったのですが、スケーリング前に比べれば劇的な精度向上です。ただ、k値を増やしていくとモデルがシンプルになり精度は下がっていくので、このままではk=9以上の精度にするのは厳しそうです。
ここでもう一つのハイパーパラメータを思い出してください。ユークリッド距離に代わってマンハッタン距離も試してみます。
Optimal k: 16
Best Test Score: 0.7151603094731716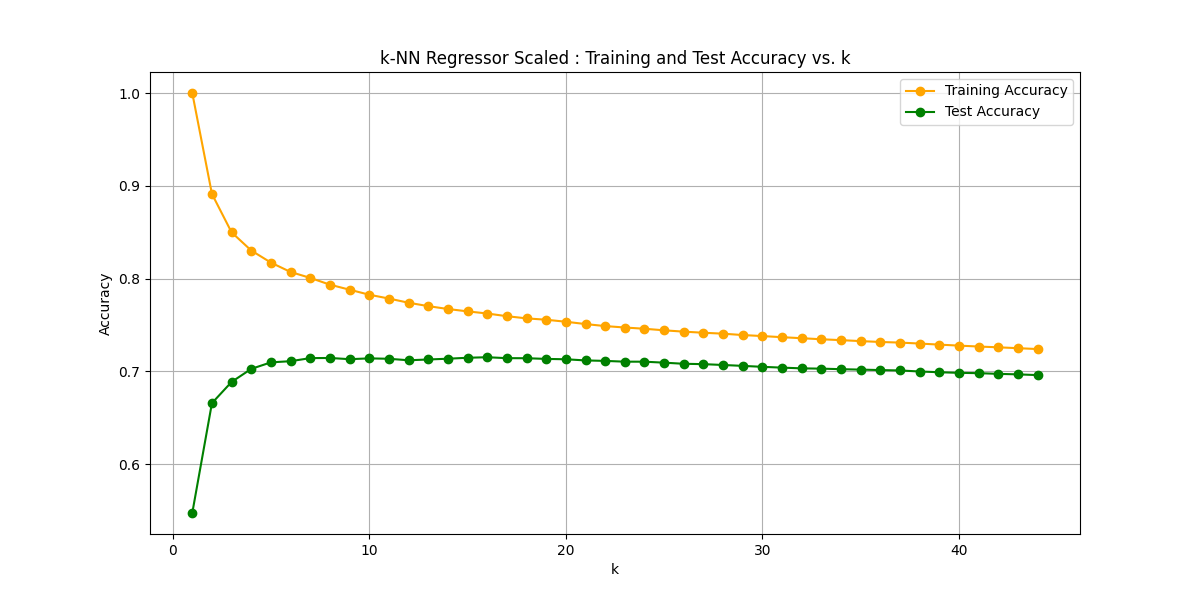
少し改善されました。
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
import pandas as pd
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['Target'] = data.target
scaler = StandardScaler()
scaled_features = scaler.fit_transform(df.drop(columns='Target'))
df_scaled = pd.DataFrame(scaled_features, columns=data.feature_names)
df_scaled['Target'] = df['Target']
plt.figure(figsize=(14, 10))
for i, col in enumerate(data.feature_names):
plt.subplot(3, 3, i + 1)
plt.scatter(df_scaled[col], df_scaled['Target'], alpha=0.5)
plt.title(f'{col} vs Target')
plt.xlabel(col)
plt.ylabel('Target')
plt.tight_layout()
plt.show()
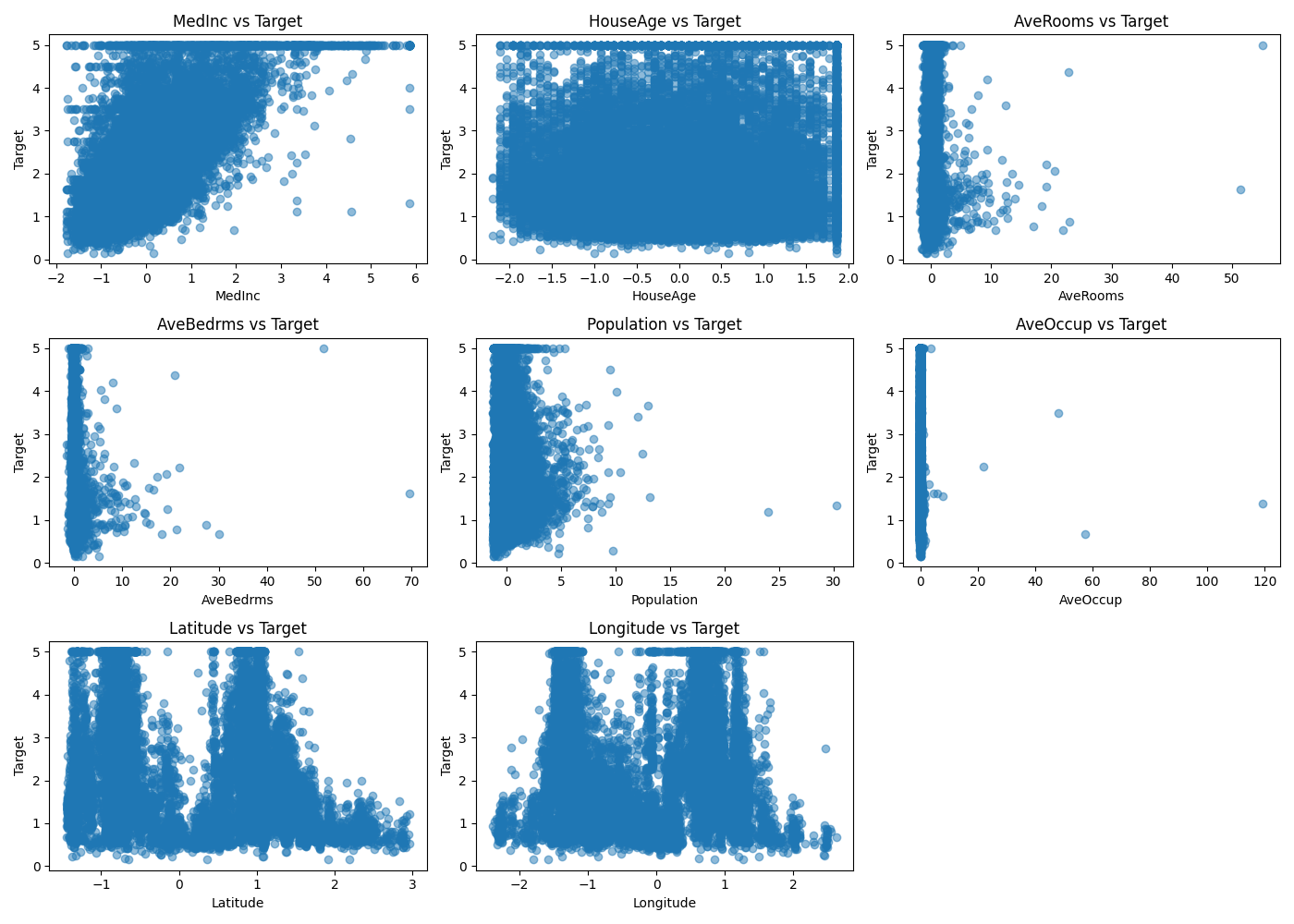
StandardScalerを噛ませた後の散布図です。スケールは不均一を解消しましたが、データの分布自体はとても差異があります。
マンハッタン距離は特徴量の差の絶対値の和を取るため、分布の影響を過大評価しなくなるのではないかと考察します。
■おわりに
k-NNを(比較的)高次元データセットでのクラス分類に適用し、その精度の高さを実感しました。また分布がありスケールが不均一なデータセットで回帰モデルを構築してみました。
今回のスコアを上回るには、特徴量エンジニアリングと呼ばれる手法や特徴量の削減(評価的な選択)が有効みたいです。またk-NNにお世話になる際にはもっと活かしてあげられるようになっていることを願って、k-最近傍法を終わりたいと思います。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- k近傍法アルゴリズムとは. ibm.com. https://www.ibm.com/jp-ja/topics/knn
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html