AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day7
経緯についてはこちらをご参照ください。
■本日の進捗
●SciPy User Guideを修了
■SciPyとは何か
「Pythonではじめる機械学習」によると下記のように紹介されている。
“SciPyは、Pythonで科学技術計算を行うための関数を集めたものである。高度な線形代数ルーチンや、数学関数の最適化、信号処理、特殊な数学関数、統計分布などの機能を持つ。”
Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
■なぜSciPyなのか
NumPy, pandas, matplotlib同様にオープンソースで、NumPyベースで構築されているためこれらのライブラリとの連携が強い。SciPyは内部メモリで処理を閉じているので大規模データに対しては制約があるものの、CとFortranで数値計算を行うため処理自体は高速。並列処理にはDaskを併用することが推奨される。深層学習にはTensorFlowやPyTorchが人気だが、それ以外の領域や数学、物理、統計などの科学技術計算においては根強い人気を誇る。
■User Guide
User Guideを順番に読んでいく。
●Special functions
scipy.specialモジュールは多くの特殊関数に対応していて、これらのほとんどが配列を引数として処理をして、結果として配列を返します。特殊関数を使うほどでもない場合は、(scipy.specialでも可能ではあるが)scipy.statsモジュールにアクセスすることが推奨されています。
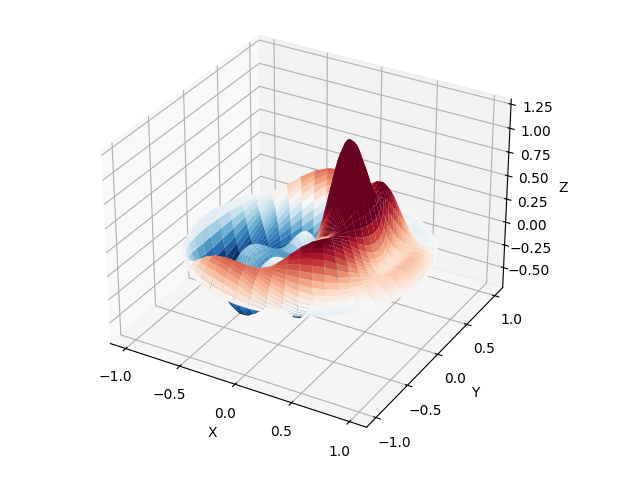
まずは、実数または複素数のオーダーαに対するベッセル微分方程式の解であるベッセル関数を用いて、円形ドラムヘッドの端部を固定した境界条件での振動モード解析を行います。
$$ x^2 \frac{ d^2 y }{ dx^2 } + x \frac{ dy }{ dx } + (x^2-\alpha^2)y = 0 $$
>>> from scipy import special
>>> import numpy as np
>>>
>>>
>>> def drumhead_height_complex(n_list, k_list, distance, angle, t):
... height = np.zeros_like(angle)
... for n, k in zip(n_list, k_list):
... kth_zero = special.jn_zeros(n, k)[-1]
... height += np.cos(t) * np.cos(n * angle) * special.jn(n, distance * kth_zero)
... return height
...
>>> n_list = [1, 2, 3]
>>> k_list = [1, 2, 3]
>>> z = np.array([drumhead_height_complex(n_list, k_list, r, theta, 0.5) for r in radius])
>>>
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_axes(rect=(0, 0.05, 0.95, 0.95), projection='3d')
>>> ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='RdBu_r', vmin=-0.5, vmax=0.5)
<mpl_toolkits.mplot3d.art3d.Poly3DCollection object at 0x0000020894FFEA20>
>>> ax.set_xlabel('X')
Text(0.5, 0, 'X')
>>> ax.set_ylabel('Y')
Text(0.5, 0.5, 'Y')
>>> ax.set_xticks(np.arange(-1, 1.1, 0.5))
[<matplotlib.axis.XTick object at 0x0000020894FFF470>, <matplotlib.axis.XTick object at 0x0000020894FF2AE0>, <matplotlib.axis.XTick object at 0x0000020894FFB740>, <matplotlib.axis.XTick object at 0x00000208950070B0>, <matplotlib.axis.XTick object at 0x0000020895007A10>]
>>> ax.set_yticks(np.arange(-1, 1.1, 0.5))
[<matplotlib.axis.XTick object at 0x0000020895004560>, <matplotlib.axis.XTick object at 0x0000020894FFA450>, <matplotlib.axis.XTick object at 0x0000020895008C20>, <matplotlib.axis.XTick object at 0x00000208950064E0>, <matplotlib.axis.XTick object at 0x0000020895009280>]
>>> ax.set_zlabel('Z')
Text(0.5, 0, 'Z')
>>> plt.show()非負整数であるベッセル関数の次元nとゼロ点kを直接指定することで、作為的に複雑な伝播を描けます。
●Python関数のオーバーヘッド
#avoiding-python-function-overheadではPythonとCythonでそれぞれループさせた実行速度の差は100マイクロセカンド以上になるという結果が示されていて、数値解析の処理の中でいちいちPythonに処理をさせるような呼び出し方を行うとPythonの遅さに引きずられてパフォーマンスが悪くなるとの注意書きがあります。
●雑魚キャラ「SciPy様のお手を煩わせるまでもございません。わたくしが対処してご覧に差し上げましょう。」
一部の簡単な関数はscipy.specialには含まれておらず、その理由としてはNumPyで簡単に実装できる他、同じ機能を持つ関数が複数実装されることを防ぐためというSciPyの基本的な方針のようです。
具体的には、多項式演算(numpy.polyid)、因数分解(primt)、トラぺゾイド法を用いた積分(numpy.trapz)、導関数の近似勾配(numpy.gradient)、コリレーション(numpy.correlate)などがあります。
●数値積分の限界値
scipy.integrateのアルゴリズムではサンプルを有限点で行うため、任意の積分関数や積分区間に対しては精度保証ができない。
ガウス積分を例にとって、下記の区間で積分する場合には理論的な結果に非常に近い結果が得られる
$$ \int_{-\infty}^{+\infty} e^{ -x^2 }dx = \sqrt{\pi} $$
>>> import scipy.integrate as integrate
>>> def gaussian(x):
... return np.exp(-x**2)
...
>>> res = integrate.quad(gaussian, -np.inf, np.inf)
>>> res
(1.7724538509055159, 1.4202636756659625e-08)結果は 1.7724538509055159 となり、推定誤差は 1.4202636756659625e-08 と非常に良い値を示している。
では、有限かつ大きな範囲で積分してみるとどうだろうか?
$$ \int_{-10000}^{+10000} e^{ -x^2 }dx $$
>>> res = integrate.quad(gaussian, -10000, 10000)
>>> res
(1.975190562208035e-203, 0.0)
>>>積分範囲を広げた結果、数値的に安定しないことが示された。ここで推定誤差が 0.0 になっているのは、何か計算精度的な問題があるのかもしれない。
積分範囲を有限で重要な部分だけにすれば安定した値を返してくれる。
$$ \int_{-15}^{+15} e^{ -x^2 }dx $$
>>> res = integrate.quad(gaussian, -15, 15)
>>> res
(1.772453850905516, 8.476526631214648e-11)
>>>●グローバル最適化
指定した範囲内における関数のグローバルミニマムを見つけ、局所的に最小値が複数存在する複雑な関数に対して全体の最適解を見つけることができます。
下記のロゼンブロック関数に対して最適解を求めて行きたいと思います。
$$ f(x, y) = (a-x)^2 + b(y-x^2)^2 $$
$$ (a=1, \ b=100)$$
>>> import numpy as np
>>> from scipy.optimize import differential_evolution
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>>
>>> def rosenbrock(x):
... a, b = 1, 100
... return (a - x[0])**2 + b * (x[1] - x[0]**2)**2
...
>>> bounds = [(-2, 2), (-1, 3)]
>>> result = differential_evolution(rosenbrock, bounds)
>>>
>>> x = np.linspace(-2, 2, 400)
>>> y = np.linspace(-1, 3, 400)
>>> xgrid, ygrid = np.meshgrid(x, y)
>>> zgrid = rosenbrock([xgrid, ygrid])
>>>
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> ax.plot_surface(xgrid, ygrid, zgrid, cmap='viridis')
<mpl_toolkits.mplot3d.art3d.Poly3DCollection object at 0x0000020894FF8F20>
>>> ax.scatter(result.x[0], result.x[1], result.fun, color='r') # Optimal point
<mpl_toolkits.mplot3d.art3d.Path3DCollection object at 0x0000020899320EC0>
>>> ax.set_xlabel('x')
Text(0.5, 0, 'x')
>>> ax.set_ylabel('y')
Text(0.5, 0.5, 'y')
>>> ax.set_zlabel('rosenbrock(x, y)')
Text(0.5, 0, 'rosenbrock(x, y)')
>>> plt.show()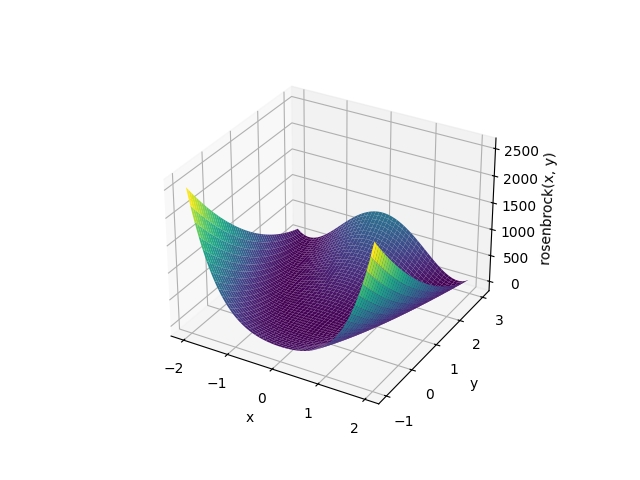
結果は下記の通り。
>>> result.fun
np.float64(0.0)
>>> result.x
array([1., 1.])
>>>●乱数シードバイアス
乱数シードに対して一般的な値(例えば0)は避けるべきで、多くの人が同じシードを使うと生成される乱数にバイアスが生じる可能性があるとのことです。シードの取り方としては、numpy.random.SeedSequenceを使うことを推奨していて、entropyを併用することでシードの乱雑さを確認できるとしています。
>>> from numpy.random import SeedSequence
>>> print(SeedSequence().entropy)
164227223893589401661391455861839720519バイアスがかかる要因は、再現性による偏りももちろんありますが、乱数生成器の状態空間が狭くなり、ある特定の状態にアクセスできなくなることによりバイアスを引き起こすこともあるらしいです。
■おわりに
全項目を深堀はしていませんが、ざっと一通り理解できました。ただ、SciPy User Guideが一番負荷が高かったです…疲れた…。これだけはUser Guideと言えど目的を持ってリファレンス的に使う方がいいのかなと思いました。明日からは(やっと!)機械学習の基礎を学んでいきたいと思います。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- SciPy user guide – SciPy 1.14.1 documentation. docs.scipy.org. 2024. https://docs.scipy.org/doc/scipy/tutorial/index.html
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/