Weight decay

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day67

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

• Weight decayを理解

■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

今回は過学習を抑制するための手法であるWeight decayについて学んでいきます。

■Weight decay

Weight decay（荷重減衰）とは、ニューラルネットワークの学習において大きな重みを持つことに対してペナルティを課すことで、モデルの複雑さを制御して過学習を防ぎ、汎化性能を向上させる手法です。

$$ L = L + \frac{1}{2} \lambda \boldsymbol{W}^2 $$

これは以前機械学習のペナルティでも学んだL2正規化と同じことですが、ニューラルネットワークではWeight decayと呼ばれています。

ちなみに逆伝播の場合は下記のようになります。

$$ \frac{\partial }{\partial \boldsymbol{W}_i} \left( \frac{1}{2} \lambda \sum_i \boldsymbol{W}_i^2 \right) = \lambda \boldsymbol{W}_i $$

アルゴリズムも実装もとても簡単なので、ニューラルネットワークに加えてみます。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = np.maximum(0, x)
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        dx = np.dot(dout, self.W.T)
        return dx

class SoftmaxCrossEntropy:
    def __init__(self):
        self.output = None
        self.grad_input = None

    def forward(self, logits):
        exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
        self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        return self.output

    def backward(self, y_true):
        self.grad_input = self.output - y_true
        return self.grad_input

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

def weight_decay(weights, weight_decay_lambda):
    return 0.5 * weight_decay_lambda * np.sum(weights ** 2)

class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01, weight_decay_lambda=0.001):
        self.params = {}
        self.weight_decay_lambda = weight_decay_lambda
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        self.layers = [
            Affine(self.params['W1'], self.params['b1']),
            ReLU(),
            Affine(self.params['W2'], self.params['b2']),
            ReLU(),
            Affine(self.params['W3'], self.params['b3'])
        ]
        self.loss_layer = SoftmaxCrossEntropy()

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def compute_loss(self, x, y_true):
        logits = self.forward(x)
        loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
        weight_decay_loss = 0
        for layer in self.layers:
            if isinstance(layer, Affine):
                weight_decay_loss += weight_decay(layer.W, self.weight_decay_lambda)
        return loss + weight_decay_loss

    def backward(self, y_true):
        dout = self.loss_layer.backward(y_true)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)

    def update(self, lr):
        for layer in self.layers:
            if isinstance(layer, Affine):
                layer.W -= lr * layer.dW
                layer.b -= lr * layer.db

    def accuracy(self, x, y_true):
        logits = self.forward(x)
        y_pred = np.argmax(logits, axis=1)
        y_true_labels = np.argmax(y_true, axis=1)
        return np.mean(y_pred == y_true_labels)

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

train_size = X_train.shape[0]
batch_size = 100
epochs = 20
np.random.seed(8)

lr = 0.001
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)

train_accuracy_history = []
test_accuracy_history = []

for epoch in range(epochs):
    for _ in range(train_size // batch_size):
        batch_mask = np.random.choice(train_size, batch_size)
        X_batch = X_train[batch_mask]
        y_batch = y_train[batch_mask]

        network.compute_loss(X_batch, y_batch)

        network.backward(y_batch)

        network.update(lr)

    train_accuracy = network.accuracy(X_train, y_train)
    test_accuracy = network.accuracy(X_test, y_test)
    train_accuracy_history.append(train_accuracy)
    test_accuracy_history.append(test_accuracy)

    print(f"Epoch {epoch+1}, Train Accuracy: {train_accuracy}, Test Accuracy: {test_accuracy}")

plt.plot(range(1, epochs + 1), train_accuracy_history, label="Train Accuracy", color="orange")
plt.plot(range(1, epochs + 1), test_accuracy_history, label="Test Accuracy", color="green")
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.title("Backpropagation SGD with Weight decay")
plt.legend()
plt.show()

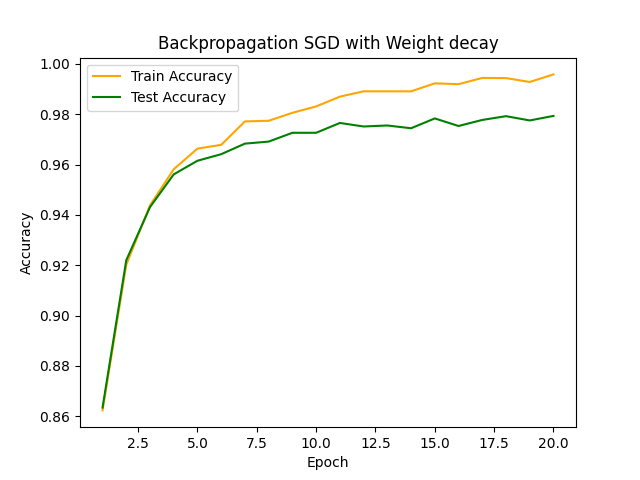
劇的な変化は確認できませんが、これまで何度も見てきた確率的勾配降下法の結果はもともと過学習の傾向は低そうなのでそんなものでしょうか。

λを0にしておけば無効化できるので、学習段階ではとりあえず入れておいて損はないかと思います。

■おわりに

ペナルティ項に1/2がかかっているのは、微分した時にシンプルな形になるからです。え、2が残るのと0.5かけるの複雑さは大体同じじゃないか？笑

■参考文献

1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
2. 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
3. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
4. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html
5. PyTorch documentation. pytorch.org. https://pytorch.org/docs/stable/index.html