AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day65
経緯についてはこちらをご参照ください。
■本日の進捗
- Xavier初期化を理解
- He初期化を理解
■はじめに
今回も「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装(オライリー・ジャパン)」で、深層学習を学んでいきます。
今回はニューラルネットワークのパラメータとしても重要な重みの初期値について、その影響と対策手法を学んでいきます。
■重みの初期値
まずは、これまで構築してきたニューラルネットワークのプログラムで何気なく書いていた、__init__関数内での重みの初期化について振り返ります。
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
このNeuralNetworkクラスの__init__関数では、重みW1, W2, W3に対してランダム配列に対して、標準偏差(weight_init_std)0.01をかけています。これは、一般に重みが小さい値の方が過剰適合(過学習)が起こりづらいと言われているからです。
それでは初期値を最も小さい値、つまり0にするとどうなるのでしょうか。実際にMNISTデータセットに対して重みの初期値を標準偏差0.01にした場合と、0にした場合で比較してみたいと思います。
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist
class ReLU:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = np.maximum(0, x)
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = np.dot(dout, self.W.T)
return dx
class SoftmaxCrossEntropy:
def __init__(self):
self.output = None
self.grad_input = None
def forward(self, logits):
exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
return self.output
def backward(self, y_true):
self.grad_input = self.output - y_true
return self.grad_input
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta)) / y.shape[0]
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, weight_init_value=0):
self.params = {}
self.params['W1'] = np.full((input_size, hidden_size), weight_init_value)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.full((hidden_size, hidden_size), weight_init_value)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = np.full((hidden_size, output_size), weight_init_value)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)
lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
loss_history = []
for i in range(step_num):
batch_mask = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_mask]
y_batch = y_train[batch_mask]
loss = network.compute_loss(X_batch, y_batch)
loss_history.append(loss)
network.backward(y_batch)
network.update(lr)
print(f"Step {i+1}, Loss: {loss}")
plt.plot(range(1, step_num + 1), loss_history)
plt.ylim(-0.1, 2.5)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("backpropagation initialize const_0")
plt.show()
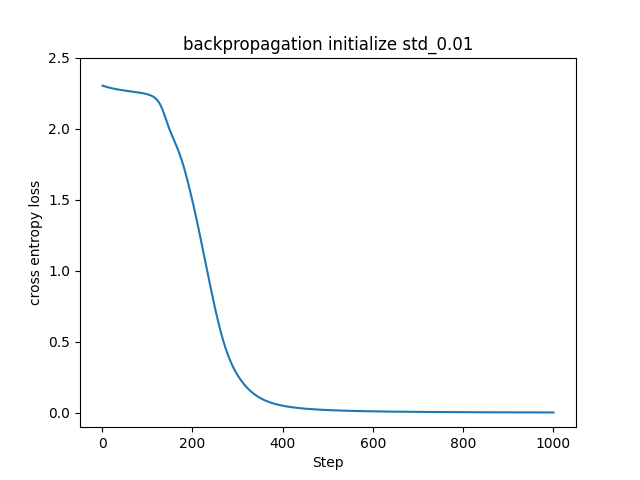
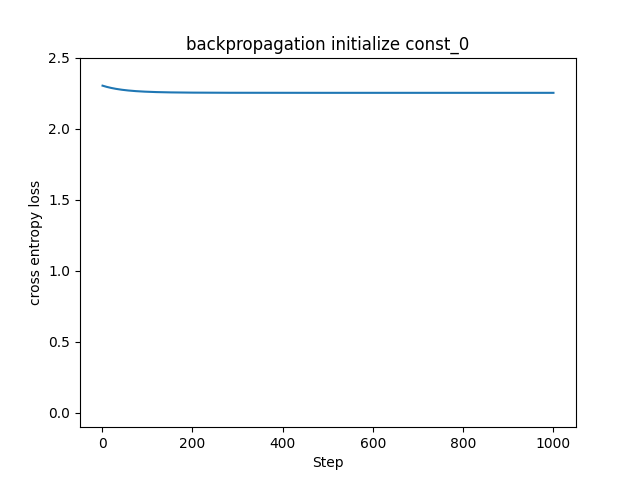
振動が乗らないようにミニバッチ学習を止めて、教師データに同一のデータを使い続ける手法に切り替えました。標準偏差0.01で初期化した左図はこれまで見てきたものと同様に損失関数の値が下がって学習が進んでいますが、0で初期化した右図は全く学習できていません。これは、全ての重みが同じ値であることが原因です。全ての重みが同じということは、更新される値も同じということです。これでは層を重ねて大量のニューロンで学習させる意味がなくなってしまいます。
もちろん、全て同じ値だと0以外でもNGです。全ての重みを0.01で初期化してみます。
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist
class ReLU:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = np.maximum(0, x)
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = np.dot(dout, self.W.T)
return dx
class SoftmaxCrossEntropy:
def __init__(self):
self.output = None
self.grad_input = None
def forward(self, logits):
exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
return self.output
def backward(self, y_true):
self.grad_input = self.output - y_true
return self.grad_input
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta)) / y.shape[0]
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, weight_init_value=0.01):
self.params = {}
self.params['W1'] = np.full((input_size, hidden_size), weight_init_value)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.full((hidden_size, hidden_size), weight_init_value)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = np.full((hidden_size, output_size), weight_init_value)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)
batch_mask = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_mask]
y_batch = y_train[batch_mask]
lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
loss_history = []
for i in range(step_num):
loss = network.compute_loss(X_batch, y_batch)
loss_history.append(loss)
network.backward(y_batch)
network.update(lr)
print(f"Step {i+1}, Loss: {loss}")
plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.ylim(-0.1, 8.0)
plt.title("backpropagation initialize const_0.01")
plt.show()
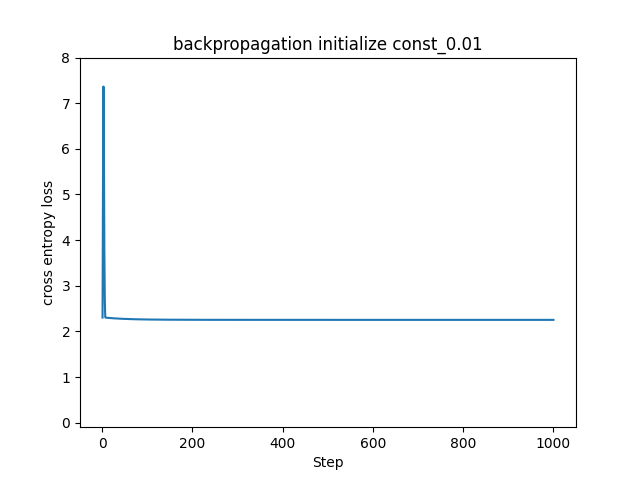
この場合も同様に学習できていません。
■Xavier初期化
適切な重みの初期化手法に関して、Xavier(Glorot)初期化という手法があります。この手法はXavier Glorotさんが発表したので、Xavier初期化ともGlorot初期化とも呼ばれます。
$$ \boldsymbol{W} \sim \mathcal{N} \left( 0, \frac{1}{n_{in} + n_{out}} \right) $$
N(0, σ2)は平均0で分散σ2の正規分布で、ガウス分布に基づいて初期化しています。運用上、前の層にあるニューロン(nin)を参照して分散を下記のように置くこともできます。
$$ \boldsymbol{W} \sim \mathcal{N} \left( 0, \frac{1}{n_{in}} \right) $$
つまり標準偏差は次のように記述できます。
$$ \frac{1}{\sqrt{n_{in}}} $$
実際に実装してみます。
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
self.params = {}
self.params['W1'] = np.random.randn(input_size, hidden_size) * np.sqrt(1 / input_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.random.randn(hidden_size, hidden_size) * np.sqrt(1 / hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = np.random.randn(hidden_size, output_size) * np.sqrt(1 / hidden_size)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
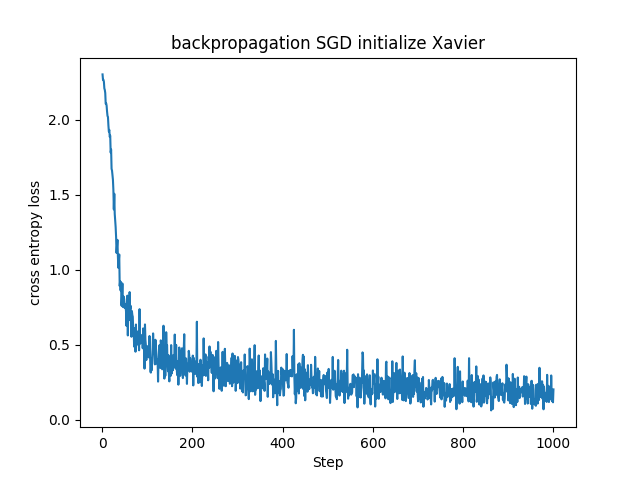
Xavier初期化は本来Sigmoid関数やtanh関数などの活性化関数に対して有効と言われています。これらの活性化関数は入力が大きく(または小さく)なると勾配が急激に小さくなるという勾配消失を起こしやすいのですが、Xavier初期化は重みが適切な範囲にスケーリングされるため相性がいいです。
■He初期化
He初期化はKaiming Heさんが推奨する手法で、重みを下記のように初期化します。
$$ \boldsymbol{W} \sim \mathcal{N} \left( 0, \frac{2}{n_{in}} \right) $$
He初期化での標準偏差は下記の通りです。
$$ \sqrt{\frac{2}{n_{in}}} $$
こちらも同様に実装してみます。
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
self.params = {}
# He初期化
self.params['W1'] = np.random.randn(input_size, hidden_size) * np.sqrt(2 / input_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.random.randn(hidden_size, hidden_size) * np.sqrt(2 / hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = np.random.randn(hidden_size, output_size) * np.sqrt(2 / hidden_size)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
def update(self, lr):
for layer in self.layers:
if isinstance(layer, Affine):
layer.W -= lr * layer.dW
layer.b -= lr * layer.db
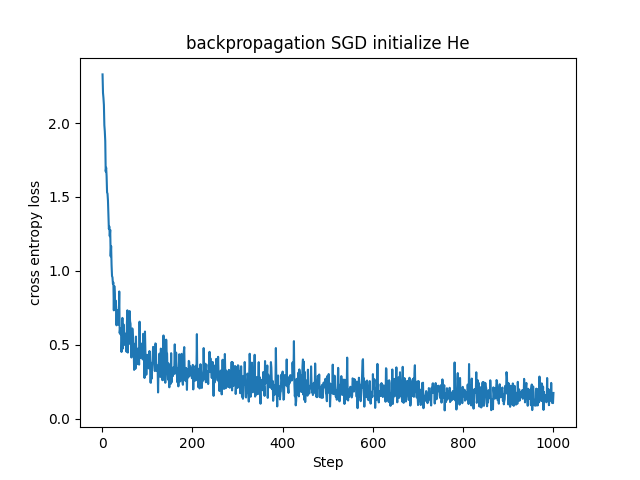
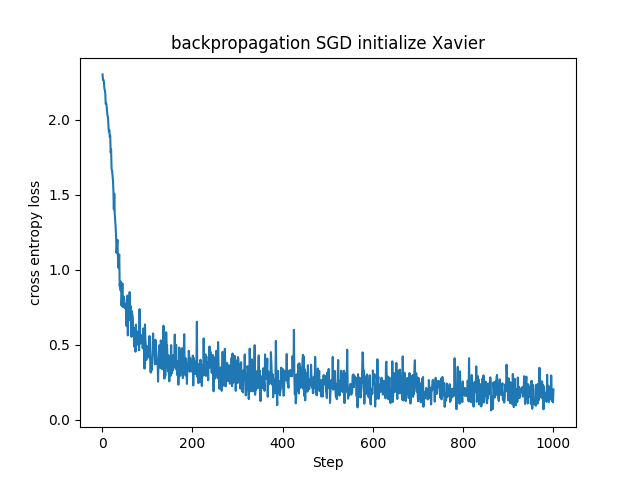
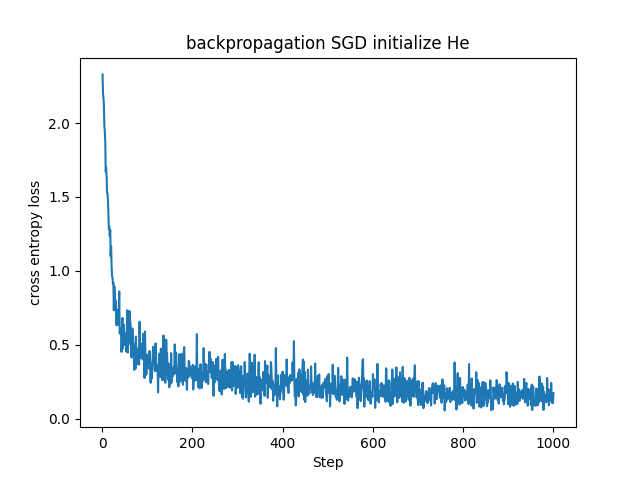
若干ですが、Xavier初期化を用いた場合よりもHe初期化を用いた場合の方が損失関数の値が急速に、かつ早く下がっています。ReLUでは入力が正である時のみニューロンが反応し、負の場合は勾配が0になります。そのため出力の分散が非対称になるのでより大きい初期分散が適しています。ReLU層を使ったニューラルネットワークではHe初期化の方が良かったのもこのためでしょうか。
■おわりに
重みの初期値によって学習速度のみならず、収束性まで変わってしまうことが分かりました。つまり初期値の選び方によって学習の結果までが変わってしまうということです。
また、お気付きの方もいるかもしれませんが、ニューラルネットワークに対するハイパーパラメータがひとつ減っています。標準偏差を指定していた場合(実際にこれまでのモデルは0.01を指定していました)、この値に対する最適化が必要な可能性がありますが、Xavier初期化やHe初期化を用いるのであれば(モデルが適切に学習できるかどうかは置いておいて)指定しないといけないパラメータは特にありません。これは個人(または小規模)でモデルを学習させる場合の計算コストに良い影響を与えそうです。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html
- PyTorch documentation. pytorch.org. https://pytorch.org/docs/stable/index.html