Adam

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day64


経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0



■本日の進捗

  • Adamを理解


■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

これまでSGDの改良版として、勾配に速度を持たせたMomentumや、学習率の自動調整をしてくれるAdaGrad、RMSPropを学んできました。今回はこれらを更に発展させた現在の機械学習界隈でも主流なAdamを学んでいきます。

■Adam

Adam（adaptive moment estimation）とは、MomentumとRMSPropの機能を持つ最適化アルゴリズムで、勾配の方向を安定させたり局所的最小値を抜け出しやすく、学習率も自動調整できるだけでなく、バイアスも補正してくれます。

次の2つのモーメントを用いて勾配の更新量を決定します。

●1次モーメント

$$ m \leftarrow \beta_1 m + (1 – \beta_1) \frac{\partial L}{\partial \boldsymbol{W}} $$

●2次モーメント

$$ v \leftarrow \beta_2 v + (1 – \beta_2) \frac{\partial L}{\partial \boldsymbol{W}} \circ \frac{\partial L}{\partial \boldsymbol{W}} $$

β1とβ2は例のごとく減衰率で、β1=0.9, β2=0.999が推奨されています。1次モーメントはMomentumに相当し、勾配の移動平均を保持して勾配の方向を安定させます。2次モーメントはRMSPropに相当し、各パラメータ毎に学習率を自動調整します。

●バイアス補正

$$ \hat{m} \leftarrow \frac{m}{1-\beta_1} $$

$$ \hat{v} \leftarrow \frac{v}{1-\beta_2} $$

各モーメントが小さい値を取る時、勾配も小さい値になり学習が進まない可能性があります。勾配が小さくても適切にパラメータが更新されるように上記のバイアス補正を行います。

●パラメータ更新

$$ \boldsymbol{W} \leftarrow \boldsymbol{W} \ – \ \eta \frac{\hat{m}}{\sqrt{\hat{v}} + \epsilon} $$

最終的なパラメータ更新はこのようにして与えられます。

早速実装してみます。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = np.maximum(0, x)
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        dx = np.dot(dout, self.W.T)
        return dx

class SoftmaxCrossEntropy:
    def __init__(self):
        self.output = None
        self.grad_input = None

    def forward(self, logits):
        exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
        self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        return self.output

    def backward(self, y_true):
        self.grad_input = self.output - y_true
        return self.grad_input

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)

        for key in params.keys():
            self.m[key] = self.beta1 * self.m[key] + (1 - self.beta1) * grads[key]
            self.v[key] = self.beta2 * self.v[key] + (1 - self.beta2) * (grads[key] ** 2)

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        self.layers = [
            Affine(self.params['W1'], self.params['b1']),
            ReLU(),
            Affine(self.params['W2'], self.params['b2']),
            ReLU(),
            Affine(self.params['W3'], self.params['b3'])
        ]
        self.loss_layer = SoftmaxCrossEntropy()

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def compute_loss(self, x, y_true):
        logits = self.forward(x)
        loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
        return loss

    def backward(self, y_true):
        dout = self.loss_layer.backward(y_true)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)

lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
optimizer = Adam(lr)

loss_history = []

for i in range(step_num):
    batch_mask = np.random.choice(train_size, batch_size)
    X_batch = X_train[batch_mask]
    y_batch = y_train[batch_mask]

    loss = network.compute_loss(X_batch, y_batch)
    loss_history.append(loss)

    network.backward(y_batch)

    grads = {
        'W1': network.layers[0].dW, 'b1': network.layers[0].db,
        'W2': network.layers[2].dW, 'b2': network.layers[2].db,
        'W3': network.layers[4].dW, 'b3': network.layers[4].db
    }

    optimizer.update(network.params, grads)

    print(f"Step {i+1}, Loss: {loss}")

plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
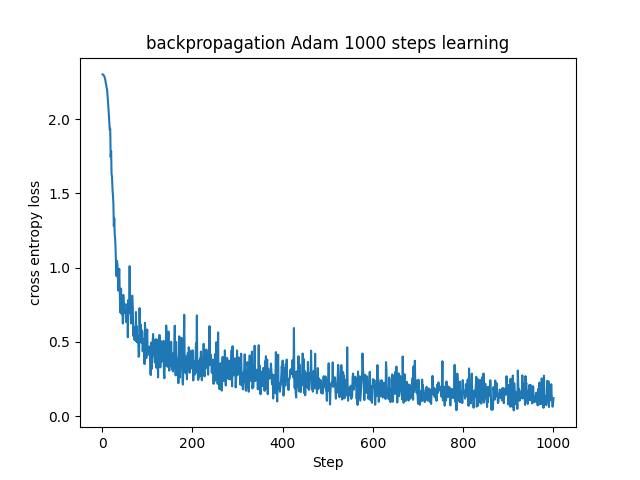
plt.title("backpropagation Adam 1000 steps learning")
plt.show()

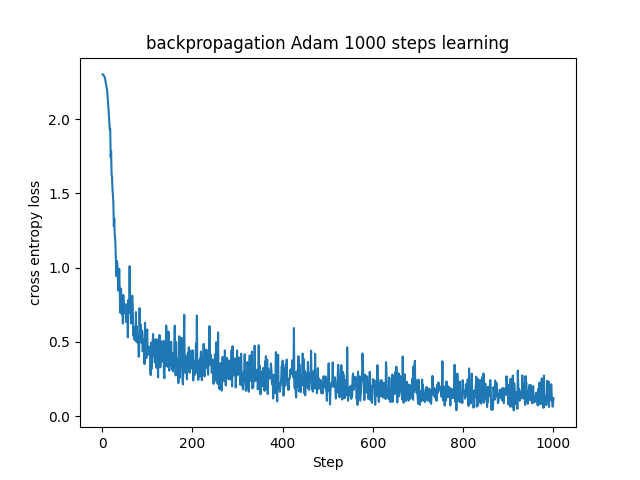
Adamは現在の機械学習界隈で良く使われる手法で、さらに発展した手法にAdaBoundという学習率にペナルティを与える手法があるものの、Adamを改良することは良き研究対象にもなっているほどです。

つまり、パラメータ更新手法としては、これまで見てきた基本的な確率的勾配降下法、Momentum、RMSProp（AdaGradの改良版）、Adamから、データセットや目的にあった選択をするというのが一般的です。

究極的には万能でハイパーパラメータを持たない（あるいは自動調整する）Optimizerを構築することが完成形と言えるでしょうか。


■確率的勾配降下法との比較

ここで、これまで学んできた手法を用いてニューラルネットワークでMNISTデータセットを学習させた様子を見てみます。

全て初期パラメータは同じです。

SGD
Momentum
RMSProp
Adam

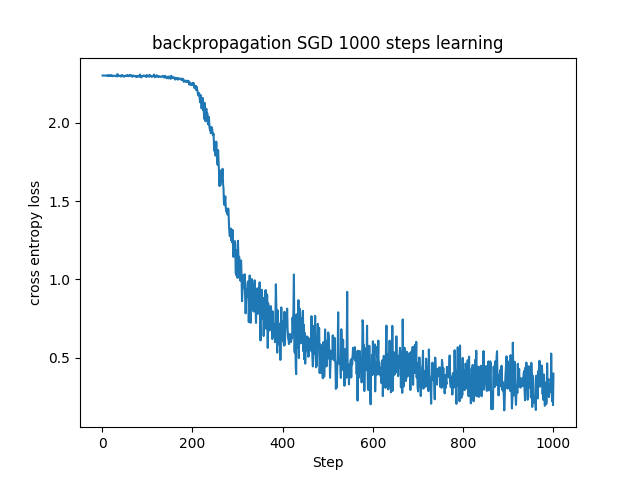
SGDは他の手法より少し学習が遅く収束に至ってなさそうに見えます。実運用する場合にはもう少しステップ数を増やした方がいいのでしょう。また、振動も大きく勾配が安定していないようです。

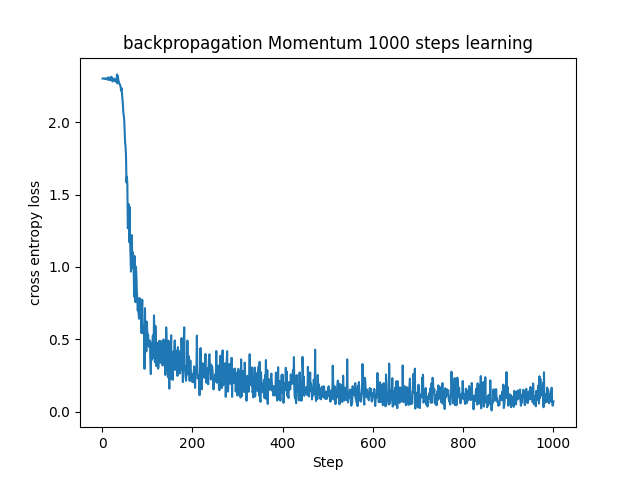
MomentumはSGDに対して振動が抑えられ、そのおかげかSGDより安定した学習をしています。

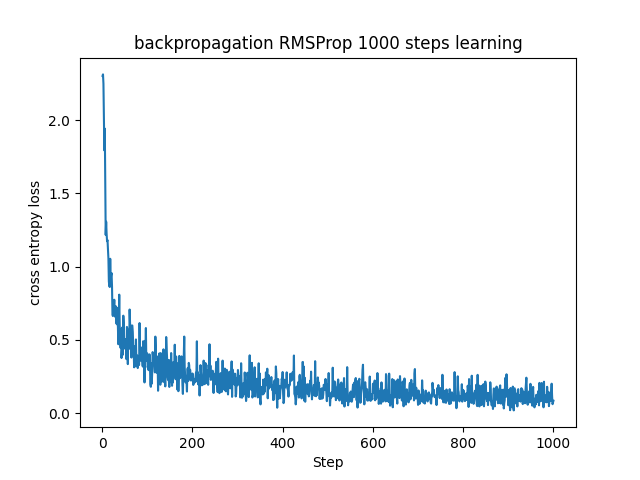
RMSPropではMomentumより早く損失関数の値が小さくなっていて、その後も比較的振動が抑えられています。

AdamはRMSPropとの違いはそれほどないですが、MomentumとRMSPropの機能を持つためか、似た学習経過を辿っているようにも見えます。

■おわりに

今回言いたいことはただ一つ。

Adamは冒頭で述べた通り、Adaptive Moment Estimationの略らしいです。
Estimationどこいった？

■参考文献

  1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
  2. 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
  3. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
  4. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html
  5. PyTorch documentation. pytorch.org. https://pytorch.org/docs/stable/index.html

hammertime

, ,
, , , ,

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です