AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day63
経緯についてはこちらをご参照ください。
■本日の進捗
- RMSPropを理解
■はじめに
今回も「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装(オライリー・ジャパン)」で、深層学習を学んでいきます。
今回は基本的な確率的勾配降下法の学習率を自動調整してくれるAdaGradの更に改良型であるRMSPropを学んでいきます。
■RMSProp
RMSProp(root mean square propagation)とは、AdaGradと同様に学習率を各パラメータ毎に調整してくれる最適化アルゴリズムですが、AdaGradと違い過去の勾配を徐々に忘れていき、最新の勾配に重きを置くように学習率を調節していきます。
$$ h \leftarrow \alpha \cdot h + ( 1 – \alpha ) \frac{\partial L}{\partial \boldsymbol{W}} \circ \frac{\partial L}{\partial \boldsymbol{W}} $$
$$ \boldsymbol{W} \leftarrow \boldsymbol{W} – \frac{\eta}{\sqrt{h + \epsilon}} \frac{\partial L}{\partial \boldsymbol{W}} $$
αは減衰率で0.9~0.99程度の値が用いられます。
AdaGrad(下記)の加算を加重和にしたものがRMSPropです。
$$ h \leftarrow h + \frac{\partial L}{\partial \boldsymbol{W}} \circ \frac{\partial L}{\partial \boldsymbol{W}} \ \ \ \ \ (※\ \mathrm{AdaGrad}の式)$$
AdaGradの欠点は学習を進めるほど(誤差を修正すればするほど)学習率が下がっていき、最終的には更新量が0になり学習が進まなくなってしまうことです。RMSPropでは単純に勾配を加算していくのではなく、指数関数的に減衰していく指数移動平均を用いることで過去の勾配スケールを減少させていくことができます。
ニューラルネットワークにRMSPropを実装してみます。
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist
class ReLU:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = np.maximum(0, x)
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = np.dot(dout, self.W.T)
return dx
class SoftmaxCrossEntropy:
def __init__(self):
self.output = None
self.grad_input = None
def forward(self, logits):
exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
return self.output
def backward(self, y_true):
self.grad_input = self.output - y_true
return self.grad_input
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta)) / y.shape[0]
class RMSProp:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] = self.decay_rate * self.h[key] + (1 - self.decay_rate) * (grads[key] ** 2)
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
self.layers = [
Affine(self.params['W1'], self.params['b1']),
ReLU(),
Affine(self.params['W2'], self.params['b2']),
ReLU(),
Affine(self.params['W3'], self.params['b3'])
]
self.loss_layer = SoftmaxCrossEntropy()
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def compute_loss(self, x, y_true):
logits = self.forward(x)
loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
return loss
def backward(self, y_true):
dout = self.loss_layer.backward(y_true)
for layer in reversed(self.layers):
dout = layer.backward(dout)
(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)
lr = 0.1
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
optimizer = RMSProp(lr)
loss_history = []
for i in range(step_num):
batch_mask = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_mask]
y_batch = y_train[batch_mask]
loss = network.compute_loss(X_batch, y_batch)
loss_history.append(loss)
network.backward(y_batch)
grads = {
'W1': network.layers[0].dW, 'b1': network.layers[0].db,
'W2': network.layers[2].dW, 'b2': network.layers[2].db,
'W3': network.layers[4].dW, 'b3': network.layers[4].db
}
optimizer.update(network.params, grads)
print(f"Step {i+1}, Loss: {loss}")
plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("backpropagation RMSProp 1000 steps learning")
plt.show()
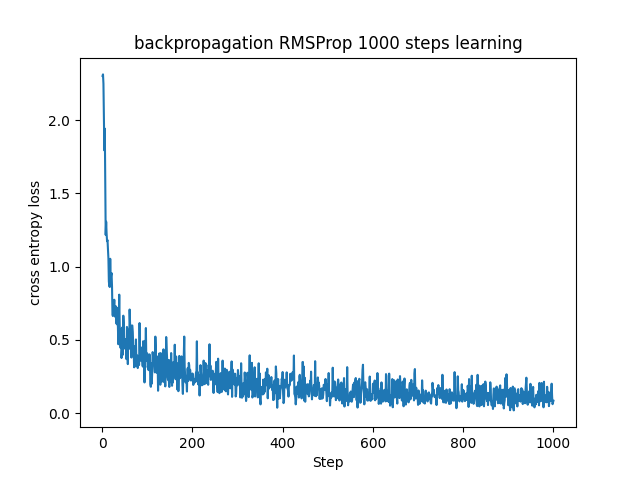
上手く学習できているように見えます。同じパラメータで学習をした場合のAdaGradとその改良版であるRMSPropを比較して見ます。
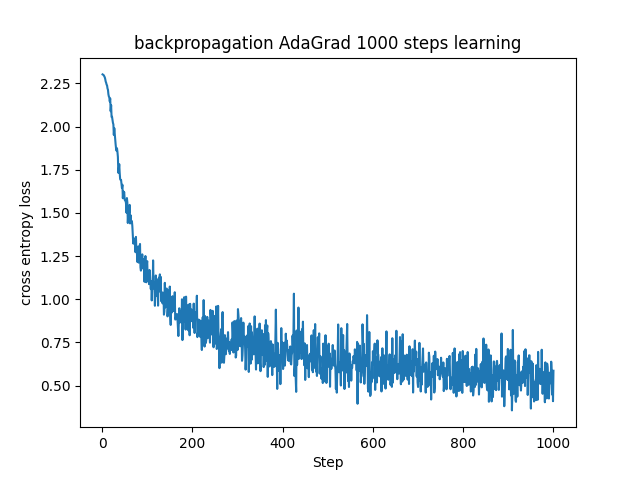
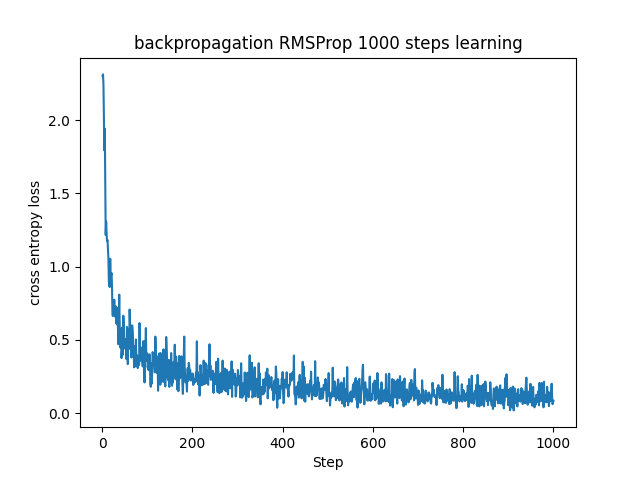
AdaGradは学習率がどんどん下がっていく傾向があるため、収束が遅い傾向があります。実際に今回のステップ数ではAdaGradの学習はまだ収束してなさそうです。RMSPropではこの傾向を抑制するように過去の勾配を忘れていくので、AdaGradに比べると学習率が非常に小さな値になることを防ぎます。今回の場合でもRMSPropは誤差が1000ステップ前には0付近に収束してきている様子が見て取れます。
■おわりに
今回は学習率を自動調節してくれるAdaGradの欠点である収束率が小さくなりすぎるという問題に対応するためにRMSPropを導入してみました。その実装自体はほとんどAdaGradと変わらないですが、より柔軟な学習率の調整ができるようになりました。
■参考文献
- Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
- 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
- ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
- API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html
- PyTorch documentation. pytorch.org. https://pytorch.org/docs/stable/index.html