AdaGrad

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day62

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

AdaGradを理解

■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

今回も前回のMomentum同様に基本的な確率的勾配降下法の改良手法として、学習率の調整を行うAdaGradを導入していきます。

■AdaGrad

AdaGrad（adaptive gradient）とは、学習率を各パラメータ毎に自動で調節してくれる最適化アルゴリズムで、過去の勾配情報を保持して、その勾配を基に学習率を都度調整します。

$$ h \leftarrow h + \frac{\partial L}{\partial \boldsymbol{W}} \circ \frac{\partial L}{\partial \boldsymbol{W}} $$

$$ \boldsymbol{W} \leftarrow \boldsymbol{W} \ – \ \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial \boldsymbol{W}} $$

損失の勾配の積はアダマール積で、行列の要素ごとの積を示します。hはこれまでの勾配の2乗和を累積していきます。更新すべきパラメータである重みに対しては、この h の平方根の逆数を学習率にかけることで、勾配が大きかったパラメータに対しては学習率を小さく、勾配が小さかったパラメータに対しては学習率を大きくすることで、学習状況に合わせてパラメータ毎に適した学習率を与えていきます。

早速、AdaGradをニューラルネットワークに実装していきます。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = np.maximum(0, x)
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        dx = np.dot(dout, self.W.T)
        return dx

class SoftmaxCrossEntropy:
    def __init__(self):
        self.output = None
        self.grad_input = None

    def forward(self, logits):
        exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
        self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        return self.output

    def backward(self, y_true):
        self.grad_input = self.output - y_true
        return self.grad_input

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        self.layers = [
            Affine(self.params['W1'], self.params['b1']),
            ReLU(),
            Affine(self.params['W2'], self.params['b2']),
            ReLU(),
            Affine(self.params['W3'], self.params['b3'])
        ]
        self.loss_layer = SoftmaxCrossEntropy()

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def compute_loss(self, x, y_true):
        logits = self.forward(x)
        loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
        return loss

    def backward(self, y_true):
        dout = self.loss_layer.backward(y_true)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)

    def update(self, lr):
        for layer in self.layers:
            if isinstance(layer, Affine):
                layer.W -= lr * layer.dW
                layer.b -= lr * layer.db

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)

lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
optimizer = AdaGrad(lr)

loss_history = []

for i in range(step_num):
    batch_mask = np.random.choice(train_size, batch_size)
    X_batch = X_train[batch_mask]
    y_batch = y_train[batch_mask]

    loss = network.compute_loss(X_batch, y_batch)
    loss_history.append(loss)

    network.backward(y_batch)

    grads = {
        'W1': network.layers[0].dW, 'b1': network.layers[0].db,
        'W2': network.layers[2].dW, 'b2': network.layers[2].db,
        'W3': network.layers[4].dW, 'b3': network.layers[4].db
    }

    optimizer.update(network.params, grads)

    print(f"Step {i+1}, Loss: {loss}")

plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("backpropagation AdaGrad 1000 steps learning")
plt.show()

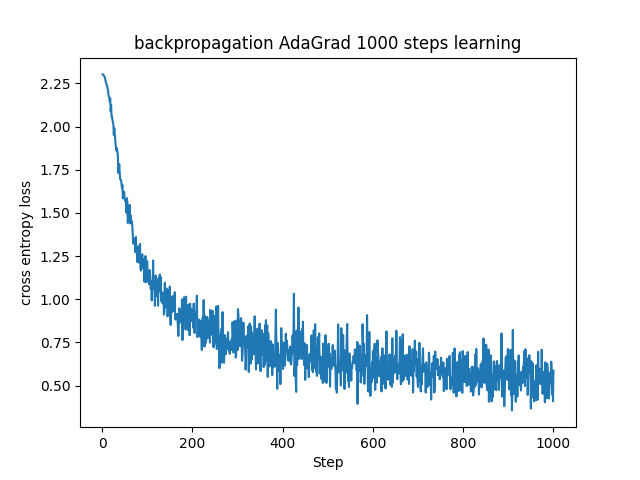
パラメータの更新（AdaGradの呼び出し）を学習ループ内に組み込みました。結果は一見SGDなどと変わらないように見えますが、AdaGradの面白いところは学習率の調整を自動で行うところです。

学習率を0.1という高めの値に設定して、SGDとAdaGradでの学習の違いを見てみたいと思います。（ソースコードは可視化を除いては lr = 0.1 に変更するだけなので割愛します。）

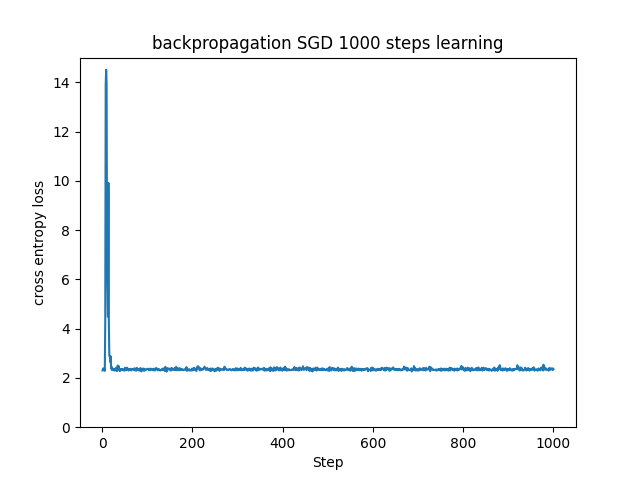
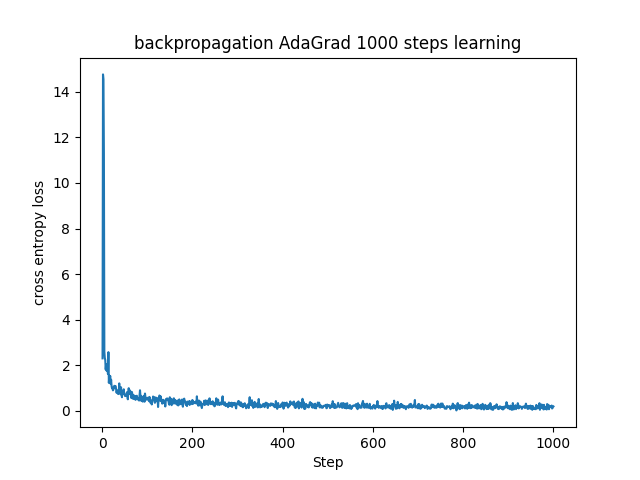
AdaGradの特徴を示した結果になりました。（だから載せているんですけどね…）

SGDでは高い学習率に対して誤差が一瞬発散しかけていますが、何とか交差エントロピー誤差が2辺りに収束して、それ以降の学習は進んでいません。

AdaGradでも最初は同様に誤差が大きくなっていますが、かなり早い段階で交差エントロピー誤差が0に近い領域に収束しています。これは序盤で勾配が大きかったパラメータに対して学習率を自動的に下げて発散傾向を抑えると共に、その後の学習も効率よく進めることができていることの表れです。

■おわりに

今回は学習率を自動調節してくれるAdaGradを試してみました。学習率をどの値にするかでSGDの結果は大きく変わってしまうことを考えると、学習率の最適化が通常は必須ですが、AdaGradを用いるだけで学習しながら調節してくれるのはとてつもなく便利だと感じました。

■参考文献

Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田秀基訳. オライリー・ジャパン. 2017. 392p.
斎藤康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html

■本日の進捗

■はじめに

■AdaGrad

■おわりに

■参考文献

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル