Momentum

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day61

経緯についてはこちらをご参照ください。

AIって結局何なのかよく分からないので、とりあえず100日間勉強してみた Day0

■本日の進捗

• Momentumを理解

■はじめに

今回も「ゼロから作るDeep Learning　Pythonで学ぶディープラーニングの理論と実装（オライリー・ジャパン）」で、深層学習を学んでいきます。

今回は確率的勾配降下法の改良手法であるMomentum を学んでいきます。

■Momentum

Momentumとは、ニューラルネットワークの学習で用いられる最適化アルゴリズムで、現在の勾配と前のステップまでの更新（速度）を利用して次の更新を行います。これにより物理学的な慣性のように勾配の方向を情報として残すので、逆方向に勾配が変動して振動するような現象を緩和することができます。

$$ \boldsymbol{ v } \leftarrow \alpha \boldsymbol{ v } \ – \ \eta \frac{\partial L}{\partial \boldsymbol{W}} $$

$$ \boldsymbol{W} \leftarrow \boldsymbol{W} + \boldsymbol{v} $$

αは外力を受けない時の減速の役割を担う抵抗係数で、勾配に学習率（η）を乗じたものとの差し引きで次の速度（v）を決定します。

早速、ニューラルネットワークの学習に組み込んでみたいと思います。

import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("./")
from work.mnist import load_mnist

class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = np.maximum(0, x)
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        dx = np.dot(dout, self.W.T)
        return dx

class SoftmaxCrossEntropy:
    def __init__(self):
        self.output = None
        self.grad_input = None

    def forward(self, logits):
        exp_values = np.exp(logits - np.max(logits, axis=1, keepdims=True))
        self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        return self.output

    def backward(self, y_true):
        self.grad_input = self.output - y_true
        return self.grad_input

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta)) / y.shape[0]

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
    
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]

class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        self.layers = [
            Affine(self.params['W1'], self.params['b1']),
            ReLU(),
            Affine(self.params['W2'], self.params['b2']),
            ReLU(),
            Affine(self.params['W3'], self.params['b3'])
        ]
        self.loss_layer = SoftmaxCrossEntropy()

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def compute_loss(self, x, y_true):
        logits = self.forward(x)
        loss = cross_entropy_error(self.loss_layer.forward(logits), y_true)
        return loss

    def backward(self, y_true):
        dout = self.loss_layer.backward(y_true)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)

    def update(self, lr):
        for layer in self.layers:
            if isinstance(layer, Affine):
                layer.W -= lr * layer.dW
                layer.b -= lr * layer.db

(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)

train_size = X_train.shape[0]
batch_size = 100
np.random.seed(8)

lr = 0.001
step_num = 1000
input_size = 784
hidden_size = 200
output_size = 10
network = NeuralNetwork(input_size, hidden_size, output_size)
momentum_optimizer = Momentum(lr=lr, momentum=0.9)

loss_history = []

for i in range(step_num):
    batch_mask = np.random.choice(train_size, batch_size)
    X_batch = X_train[batch_mask]
    y_batch = y_train[batch_mask]

    loss = network.compute_loss(X_batch, y_batch)
    loss_history.append(loss)

    network.backward(y_batch)

    grads = {
        'W1' : network.layers[0].dW,
        'b1' : network.layers[0].db,
        'W2' : network.layers[2].dW,
        'b2' : network.layers[2].db,
        'W3' : network.layers[4].dW,
        'b3' : network.layers[4].db
    }
    momentum_optimizer.update(network.params, grads)

    print(f"Step {i+1}, Loss: {loss}")

plt.plot(range(1, step_num + 1), loss_history)
plt.xlabel("Step")
plt.ylabel("cross entropy loss")
plt.title("backpropagation Momentum 1000 steps learning")
plt.show()

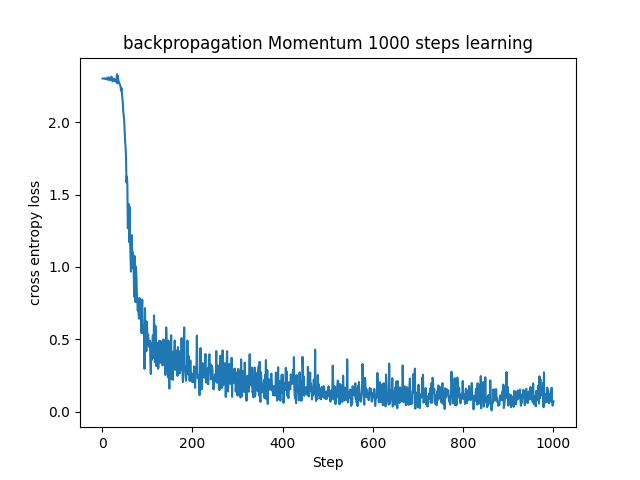
調整のため、学習率を0.001に、バッチサイズを100にしています。

これまでNeuralNetworkクラスのupdateを用いてパラメータを更新していましたが、Momentumクラスを新たに作成し、Momentumを用いてパラメータを更新するように実装しました。

同じ学習率とバッチサイズで学習させた時の、確率的勾配降下法（SGD）とMomentumの学習の様子を比較して見てみます。

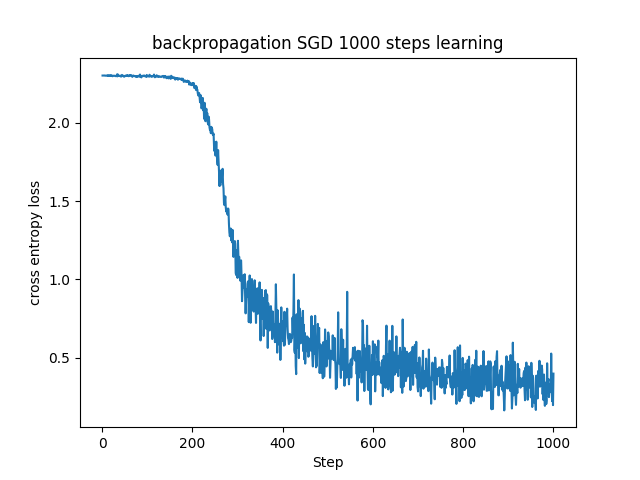
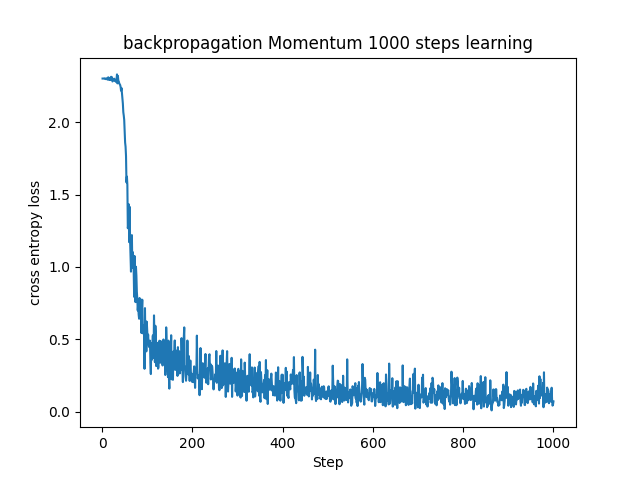
お互いに調整しろがあるので直接的な比較はできませんが、学習の仕方に違いがあることが分かるかと思います。

■おわりに

今回はパラメータの更新にMomentumを実装してみました。一般に確率的勾配降下法は小さいミニバッチやその切り替えで学習率をかけるシンプルなパラメータ更新なので振動しやすかったり、局所的最小値に閉じ込められる危険性があると言われています。Momentumは速度（慣性）を持つために勾配の振動を抑えることができ、また同様に勢いを保持するために局所的最小値から抜け出せる可能性が高くなります。

ただし、損失関数によってはSGDで十分である場合も多いことも注意しておきたいところです。

■参考文献

1. Andreas C. Muller, Sarah Guido. Pythonではじめる機械学習. 中田 秀基 訳. オライリー・ジャパン. 2017. 392p.
2. 斎藤 康毅. ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装. オライリー・ジャパン. 2016. 320p.
3. ChatGPT. 4o mini. OpenAI. 2024. https://chatgpt.com/
4. API Reference. scikit-learn.org. https://scikit-learn.org/stable/api/index.html